Topological sort is a method to sort the vertices in directed acyclic graph in which each node comes before all the nodes to which it has edges going to. Topological sort is mainly used in cases where a certain node can be visited if and only if certain nodes has been visited before.
A Directed Acyclic graph or DAG is a graph which doesn’t have any cycle.
All pairs of consecutive vertices in topological sorted order are connected by edges which forms a directed Hamiltonian Path.
Let’s have a look at sample graph on which we will apply topological sort to understand it better.
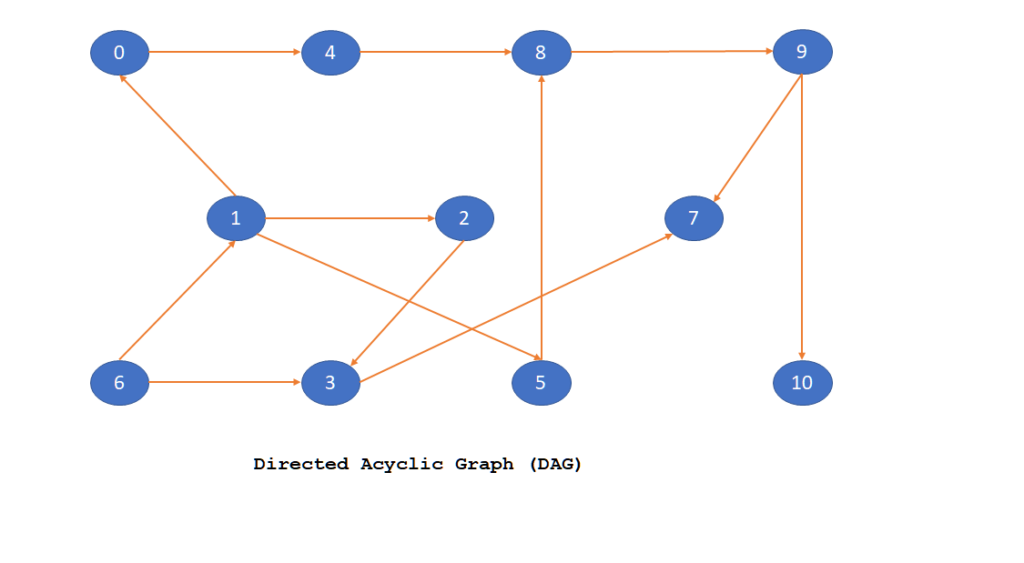
In the above example topological sort order could be “6 1 0 2 5 4 3 8 9 7 10”.
Indegree of a vertex
Indegree of a node in graph is defined as the total number of edges which are coming to the node.
For eg: in above image,
- Vertex 6 has 0 incoming edges and hence it’s indegree is “0”.
- Vertex 1 has 2 incoming edges and hence it’s indegree is “2”.
Algorithm
Algorithm to calculate topological sort is as follows:
- Calculate indegree of all the vertices.
- All vertices of indegree “0” will be pushed into a queue.
- While Queue is not empty
- Dequeue the vertex “A”.
- Reduce indegree of those vertices which have incoming edge from vertex “A”.
- If indegree of the vertices becomes 0 then Enqueue that vertex to Queue.
Before going ahead please have a look at the Graph and Its implementation.
Let’s have a look at the Graph class and it’s helper functions.
class Graph
{
private:
int m_nodes;
int m_edges;
int **edges;
bool isUndirected;
int isConnected;
public:
Graph (int nodes, bool isUndirected);
int getNumberOfNodes ();
int getNumberOfEdges ();
void getEdges ();
bool addEdge (int srcNode, int dstNode);
void BFS (int start);
void DFS (int start);
~Graph ();
bool isConnectedGraph ();
bool printMotherVertex ();
void topologicalSort ();
void getEdgesIn2DFormat ();
};
void Graph::getEdgesIn2DFormat ()
{
cout << "Printing edges in 2D format!!" << endl;
for (int i = 0; i < m_nodes; i++)
{
for (int j = 0; j < m_nodes; j++)
{
cout << edges[i][j] << " ";
}
cout << endl;
}
}
Graph::~Graph ()
{
if (!edges)
{
cout << "Graph was never initializaed, nothing to free " << endl;
return;
}
for (int i = 0; i < m_nodes; i++)
{
delete [] edges[i];
}
delete [] edges;
}
Graph::Graph (int nodes, bool isUndirected): m_nodes (nodes),
m_edges (0),
edges (NULL),
isUndirected (isUndirected),
isConnected (-1)
{
edges = new int*[m_nodes];
if (!edges)
{
cout << "Graph initialization failed " << endl;
}
for (int i = 0; i < m_nodes; i++)
{
edges[i] = new int[m_nodes];
}
for (int i = 0; i < m_edges; i++)
{
for (int j = 0; j < m_edges; j++)
{
edges[i][j] = 0;
}
}
}
int Graph::getNumberOfNodes ()
{
return m_nodes;
}
int Graph::getNumberOfEdges ()
{
return m_edges;
}
bool Graph::addEdge (int srcNode, int dstNode)
{
if (srcNode >= m_nodes || dstNode >= m_nodes)
{
cout << "srcNode " << srcNode << " or dstNode " << dstNode << " is out of known max node: " << m_nodes << endl;
return false;
}
if (edges[srcNode][dstNode])
{
cout << "srcNode " << srcNode << " or dstNode " << dstNode << " is already existed." << endl;
return false;
}
edges[srcNode][dstNode] = 1;
++m_edges;
if (isUndirected)
{
edges[dstNode][srcNode] = 1;
++m_edges;
}
return true;
}
Let’s have a look at the topological sort function.
Before going ahead, have a look at Queue and It’s implementation for better understanding of below code.
void Graph::topologicalSort ()
{
int indegree[m_nodes] = {0};
for (int i = 0; i < m_nodes; i++)
{
for (int j = 0; j < m_nodes; j++)
{
if (i == j)
continue;
if (edges[i][j])
indegree[j]++;
}
}
cout << "Printing indegree of nodes" << endl;
Queue q(m_nodes);
for (int i = 0; i < m_nodes; i++)
{
cout << indegree[i] << " ";
if (indegree[i] == 0)
{
q.enqueue (i);
}
}
cout << endl;
cout << "Printing Topological sort !!" << endl;
int counter = 0;
while (!q.isEmpty ())
{
counter++;
int node = q.dequeue ();
cout << node << " ";
for (int j = 0; j < m_nodes; j++)
{
if (node == j)
continue;
if (edges[node][j] == 1)
{
if (--indegree[j] == 0)
q.enqueue (j);
}
}
}
cout << endl;
if (counter != m_nodes)
cout << "Graph has cycles, topological sort not possible !!" << endl;
}
Let’s have a look at the main function which utilizes the above function.
void add_header (const char *line)
{
cout << "========================================================================" << endl;
cout << line << endl;
cout << "========================================================================" << endl;
}
int main ()
{
add_header ("Sorting Graph Using Topological Sort");
Graph g2(11, false);
g2.addEdge (0,4);
g2.addEdge (1,0);
g2.addEdge (6,1);
g2.addEdge (1,2);
g2.addEdge (1,5);
g2.addEdge (2,3);
g2.addEdge (6,3);
g2.addEdge (3,7);
g2.addEdge (4,8);
g2.addEdge (5,8);
g2.addEdge (9,7);
g2.addEdge (8,9);
g2.addEdge (9,10);
g2.getEdgesIn2DFormat ();
g2.topologicalSort ();
}
Let’s look at the output of above main function.
========================================================================
Sorting Graph Using Topological Sort
========================================================================
Printing edges in 2D format!!
0 0 0 0 1 0 0 0 0 0 0
1 0 1 0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 1 0 0
0 1 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1 0 0 1
0 0 0 0 0 0 0 0 0 0 0
Printing indegree of nodes
1 1 1 2 1 1 0 2 2 1 1
Printing Topological sort !!
6 1 0 2 5 4 3 8 9 7 10
Applications of Topological Sort
- Course curriculum where certain subjects can be taken only if certain subjects are already completed.
- Deadlock detection
- Pipelining of jobs