Shortest path algorithms are designed to find the minimum cost path between two nodes in a graph. This algorithm can be used to find out the fastest way to reach from one place to another or it can be used to find cheapest way to fly or travel between source and destination.
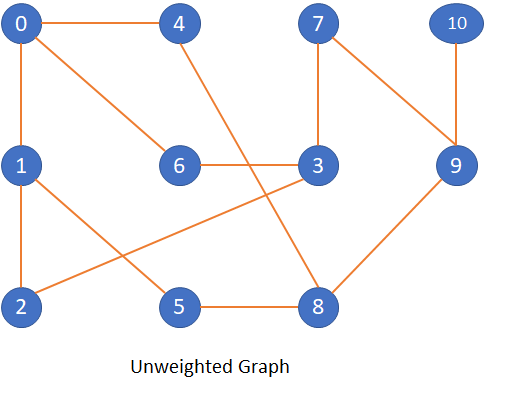
An unweighted graph is a graph in which all the edges are of same cost. In this unweighted graph, we have to find the shortest path to all the vertices from a given vertices. This algorithm is very much similar to BFS.
Before going ahead have a look into Graph Basics.
Let’s look into an unweighted graph in which we have to calculate the shortest path to all the vertices from a given node.
Algorithm
- Define a distance array of size equal to graph node and initialize it to -1.
- Define a path array of size equal to graph node and initialize it to -1.
- Pick the given graph node to start the traversal and enqueue it into a Queue.
- Set the distance for the start node as 0 and path to reach from itself.
- Dequeue the node from the Queue.
- For all the edge from the dequeued node, if distance of any neighbor node is set to “-1” then
- set distance = distance[dequeued node] + 1
- Put this neighbor node in queue.
- Update path[neighbor] = dequeued_node
- For all the edge from the dequeued node, if distance of any neighbor node is set to “-1” then
- Repeat above step till the queue is empty.
Implementation
Let’s look into a sample Graph class which we are going to use it here. Check Graph and it’s basic implementation for more details.
class Graph
{
private:
int m_nodes;
int m_edges;
int **edges;
bool isUndirected;
int isConnected;
public:
Graph (int nodes, bool isUndirected);
int getNumberOfNodes ();
int getNumberOfEdges ();
void getEdges ();
bool addEdge (int srcNode, int dstNode);
~Graph ();
void shortestPathInUnweightedGraph (int srcNode);
};
Let’s look into the function to find shortest path in unweighted graph. Please look into Queue and It’s implementation before going ahead.
void Graph::shortestPathInUnweightedGraph (int srcNode)
{
int distance[m_nodes];
int path[m_nodes];
for (int i = 0; i < m_nodes; i++) {
distance[i] = -1;
path[i] = -1;
}
Queue q(m_nodes);
q.enqueue (srcNode);
distance[srcNode] = 0;
path[srcNode] = srcNode;
while (!q.isEmpty ()) {
int cur_node = q.dequeue ();
if (distance[cur_node] == -1) {
cout << "Incorrect distance set for node: " << cur_node << endl;
}
for (int j = 0; j < m_nodes; j++) {
if (edges[cur_node][j] == 1 && distance[j] == -1) {
distance[j] = distance[cur_node] + 1;
q.enqueue (j);
path[j] = cur_node;
}
}
}
for (int i = 0; i < m_nodes; i++) {
cout <<"Node: " << i << " distance: " << distance[i] << " from Node: " << path[i] << endl;
}
}
Let’s define a sample graph and check how this code works.
int main ()
{
Graph g2(11, true);
g2.addEdge (0,4);
g2.addEdge (1,0);
g2.addEdge (6,0);
g2.addEdge (1,2);
g2.addEdge (1,5);
g2.addEdge (2,3);
g2.addEdge (6,3);
g2.addEdge (3,7);
g2.addEdge (4,8);
g2.addEdge (5,8);
g2.addEdge (9,7);
g2.addEdge (8,9);
g2.addEdge (9,10);
g2.getEdgesIn2DFormat ();
g2.topologicalSort ();
add_header ("Finding shortest path from Node 6");
g2.shortestPathInUnweightedGraph (6);
add_header ("Finding shortest path from Node 0");
g2.shortestPathInUnweightedGraph (0);
}
Let’s check the output of above code.
Printing edges in 2D format!!
0 1 0 0 1 0 1 0 0 0 0
1 0 1 0 0 1 0 0 0 0 0
0 1 0 1 0 0 0 0 0 0 0
0 0 1 0 0 0 1 1 0 0 0
1 0 0 0 0 0 0 0 1 0 0
0 1 0 0 0 0 0 0 1 0 0
1 0 0 1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 1 0
0 0 0 0 1 1 0 0 0 1 0
0 0 0 0 0 0 0 1 1 0 1
0 0 0 0 0 0 0 0 0 1 0
========================================================================
Finding shortest path from Node 6
========================================================================
Node: 0 distance: 1 from Node: 6
Node: 1 distance: 2 from Node: 0
Node: 2 distance: 2 from Node: 3
Node: 3 distance: 1 from Node: 6
Node: 4 distance: 2 from Node: 0
Node: 5 distance: 3 from Node: 1
Node: 6 distance: 0 from Node: 6
Node: 7 distance: 2 from Node: 3
Node: 8 distance: 3 from Node: 4
Node: 9 distance: 3 from Node: 7
Node: 10 distance: 4 from Node: 9
========================================================================
Finding shortest path from Node 0
========================================================================
Node: 0 distance: 0 from Node: 0
Node: 1 distance: 1 from Node: 0
Node: 2 distance: 2 from Node: 1
Node: 3 distance: 2 from Node: 6
Node: 4 distance: 1 from Node: 0
Node: 5 distance: 2 from Node: 1
Node: 6 distance: 1 from Node: 0
Node: 7 distance: 3 from Node: 3
Node: 8 distance: 2 from Node: 4
Node: 9 distance: 3 from Node: 8
Node: 10 distance: 4 from Node: 9