A tree is a data structure similar to Linked list in which each node points to multiple nodes instead of simply pointing to the next node. A tree is called Binary tree if each node in a tree has maximum of two nodes.
The lowest common ancestor of any two nodes X and Y in a binary tree is the lowest node in tree that has both X and Y node as successor.
Before going ahead have a look into Binary Tree basics, Binary Tree Traversal and Binary Tree implementation.
Let’s have a look on basic class definition for Binary Tree.
class BinaryTree
{
public:
int m_data;
BinaryTree* m_left;
BinaryTree* m_right;
BinaryTree (int data);
BinaryTree (int data, BinaryTree* left, BinaryTree* right);
~BinaryTree ();
};
void print_binary_tree (BinaryTree* root)
{
cout << " " << root -> m_data;
if (root -> m_left)
print_binary_tree (root -> m_left);
if (root -> m_right)
print_binary_tree (root -> m_right);
}
void print_tree (BinaryTree* root)
{
cout << "Binary tree contents: ";
print_binary_tree (root);
cout << endl;
}
Lowest Common Ancestor (LCA)
The lowest common ancestor of any two nodes X and Y in a binary tree is the lowest node in tree that has both X and Y node as successor. Let’s look into the below binary tree to understand it better.
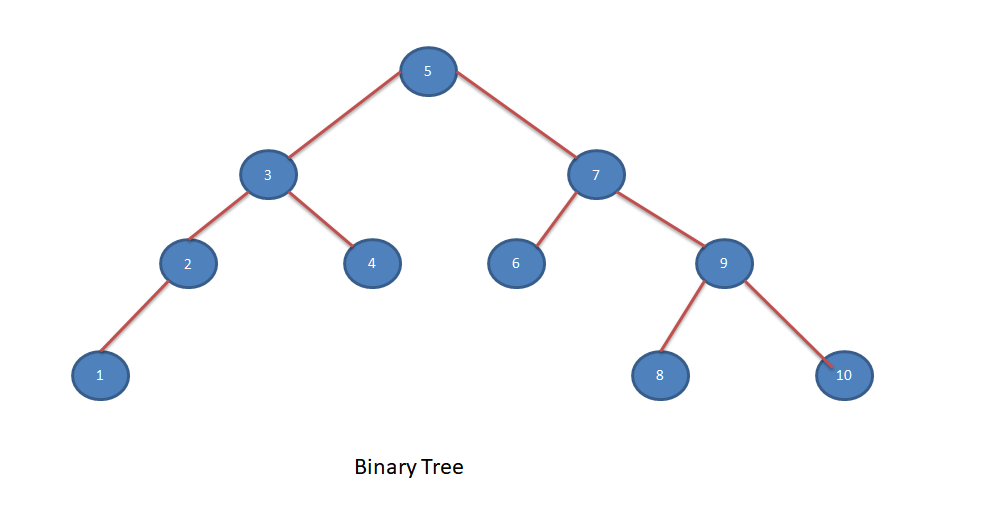
In the above tree,
- LCA of node (1,4) is 3
- LCA of node (1,2) is 2
- LCA of node (1,10) is 5
Algorithm
- Iterate the Binary Tree from Root node.
- If any of the node is root node then LCA is root node.
- If one node is in left subtree of root node and other node is in right subtree of root node then LCA is root node.
- If both node are in left or right subtree then repeat above steps using that node as root node.
Let’s look into the sample code to find out Lowest common ancestor of given nodes in a Binary Tree.
BinaryTree* find_node (BinaryTree* root, int m, int n, bool* is_found_m, bool* is_found_n)
{
if (!root)
return NULL;
if (root->m_data == m || root ->m_data == n) {
*is_found_m |= (root->m_data == m);
*is_found_n |= (root->m_data == n);
if (!*is_found_n || !*is_found_m) {
find_node (root->m_left, m, n, is_found_m, is_found_n);
find_node (root->m_right, m, n, is_found_m, is_found_n);
}
return root;
}
BinaryTree* left = find_node (root->m_left, m, n, is_found_m, is_found_n);
BinaryTree* right = find_node (root->m_right, m, n, is_found_m, is_found_n);
if (left && right)
return root;
return (left ? left : right);
}
BinaryTree* least_common_ancestor (BinaryTree* root, int m, int n)
{
if (!root)
return NULL;
if (root->m_data == m || root ->m_data == n)
return root;
bool is_m = false;
bool is_n = false;
BinaryTree* left = find_node (root->m_left, m, n, &is_m, &is_n);
BinaryTree* right = find_node (root->m_right, m, n, &is_m, &is_n);
if (!is_m || !is_n)
return NULL;
if (left && right)
return root;
return (left ? left : right);
}
Few of the functions used below are explained in Binary Tree implementation. Refer those before going ahead. Let’s define a main function to use above functions.
int main ()
{
BinaryTree* node1 = new BinaryTree (1);
BinaryTree* node2 = new BinaryTree (2);
BinaryTree* node3 = new BinaryTree (3);
BinaryTree* node4 = new BinaryTree (4);
BinaryTree* node5 = new BinaryTree (5);
BinaryTree* node6 = new BinaryTree (6);
BinaryTree* node7 = new BinaryTree (7);
BinaryTree* node8 = new BinaryTree (8);
BinaryTree* node9 = new BinaryTree (9);
BinaryTree* node10 = new BinaryTree (10);
/* Set node5 as root node */
/*
5
3 7
2 4 6 9
1 8 10
*/
BinaryTree* root = node5;
node5 -> m_left = node3;
node3 -> m_left = node2;
node3 -> m_right = node4;
node2 -> m_left = node1;
node5 -> m_right = node7;
node7 -> m_left = node6;
node7 -> m_right = node9;
node9 -> m_right = node10;
node9 -> m_left = node8;
print_tree (root);
cout << " Postorder Traversal: ";
postorder_traversal (root);
cout << endl;
BinaryTree* lca = least_common_ancestor (root, 8, 9);
cout << "LCA for node 8,9 is " << (lca ? lca->m_data: 0) << endl;
lca = least_common_ancestor (root, 1, 10);
cout << "LCA for node 1,10 is " << (lca ? lca->m_data: 0) << endl;
lca = least_common_ancestor (root, 1, 3);
cout << "LCA for node 1,3 is " << (lca ? lca->m_data: 0) << endl;
lca = least_common_ancestor (root, 8, 19);
cout << "LCA for node 8,19 is " << (lca ? lca->m_data: 0) << endl;
}
Let’s look into the output of above main function.
Binary tree contents: 5 3 2 1 4 7 6 9 8 10
Postorder Traversal: 1 2 4 3 6 8 10 9 7 5
LCA for node 8,9 is 9
LCA for node 1,10 is 5
LCA for node 1,3 is 3
LCA for node 8,19 is 0