A Binary Search Tree is a Binary tree in which all the nodes has following properties.
- Left subtree of a node contains all the nodes having values lesser than the node.
- Right subtree of a node contains all the nodes having values higher than the node.
- Both the left and right subtree is also a Binary Search Tree.
As the name suggests, this data structure is mainly used for faster searching. In order to do that, restrictions are applied while inserting/deleting an element into the tree. As a result of these restrictions, worst case search time complexity remains at O(log n). Before going ahead have a look into Binary Search Tree basics, Binary Search Tree Insert, Binary Search Tree Delete, Binary Search Tree Search operations.
Let’s have a look into basic C++ class definition for Binary Search Tree.
template <typename T>
class BinarySearchTree
{
public:
T m_data;
BinarySearchTree* m_left;
BinarySearchTree* m_right;
BinarySearchTree (T data);
~BinarySearchTree ();
};
/* Below are some useful functions which we are going to use it in our examples */
template <typename T>
void print_binary_tree_inorder (BinarySearchTree<T>* root)
{
if (root -> m_left)
print_binary_tree_inorder (root -> m_left);
cout << " " << root -> m_data;
if (root -> m_right)
print_binary_tree_inorder (root -> m_right);
}
template <typename T>
void print_tree (BinarySearchTree<T>* root)
{
cout << "Binary tree contents: ";
print_binary_tree_inorder (root);
cout << endl;
}
/* Simply used this function to delete all nodes and free memory */
template <typename T>
void delete_all_nodes (BinarySearchTree<T>* root)
{
if (!root)
return;
if (root -> m_left)
{
delete_all_nodes (root -> m_left);
}
if (root -> m_right)
{
delete_all_nodes (root -> m_right);
}
delete root;
}
Finding Kth Maximum value in a Binary Search Tree
In Binary Search Tree data is stored in a particular manner due to which inorder traversal of Binary Search Tree will provide a sorted list. Based on the property of Binary Search Tree in which left node is lower than root node which is lower than right node, we will traverse the Binary Search Tree in a manner to find out the Kth Largest Value. Inorder traversal of Binary Search Tree produces a sorted list, which can be used here.
Let’s take an example to understand the working of above algorithm to find out the 4th node with maximum value.
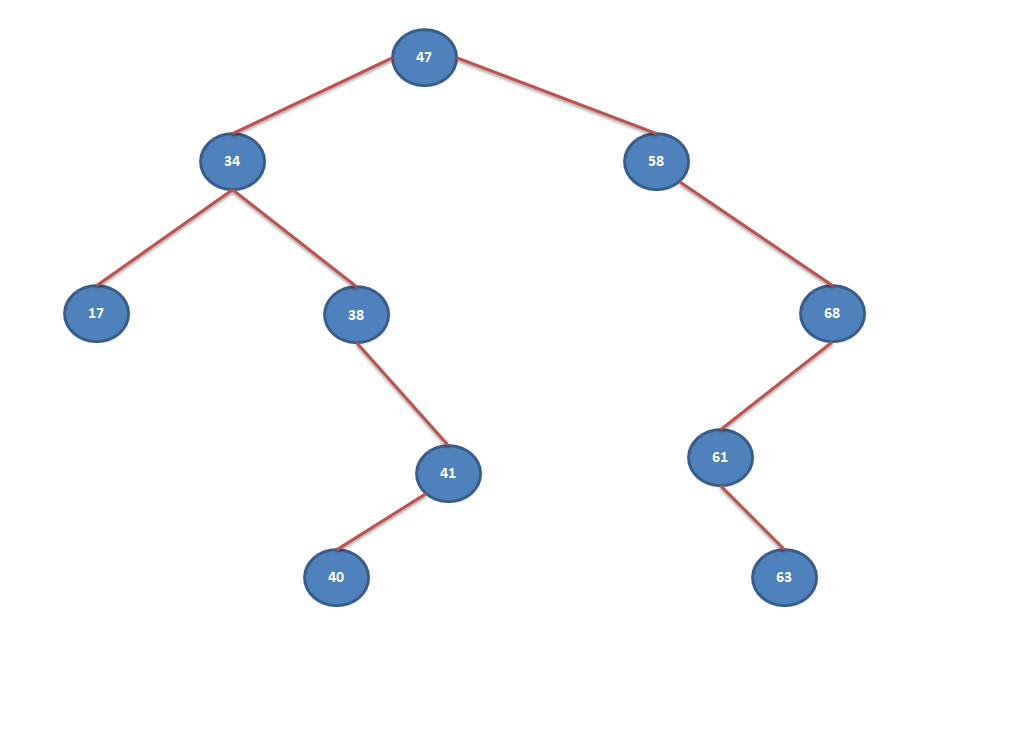
- Start with the root element “47”.
- Move towards right child “58”.
- Move towards right child “68”. This is the right most child and hence would be the largest node in BST.
- If this node “68” has a left child then go towards that otherwise move to parent node. Move towards left node “61”.
- If this node “61” has a right child then go towards that otherwise this node would be the next largest node. Move towards right node “63”.
- If this node “63” has a right child then go towards that otherwise this node would be the next largest node. Hence, this is 2nd largest node.
- if this node “63” has a left child then go towards that otherwise go to parent. Move to parent node “61”.
- This parent node “61” will be the next largest node. Hence, this is 3rd largest node.
- Move towards it’s parent node “68”.
- Move towards it’s parent node “58”. This will be the 4th largest node.
Let’s look into the sample code.
template <typename T>
BinarySearchTree<T>* find_kth_maximum_element_in_bst (BinarySearchTree<T>* root, int k, int* count)
{
if (!root)
return NULL;
BinarySearchTree<T>* temp = find_kth_maximum_element_in_bst (root -> m_right, k, count);
if (temp)
return temp;
++(*count);
if (*count == k)
return root;
return find_kth_maximum_element_in_bst (root -> m_left, k, count);
}
Few of the functions defined below are explained in Binary Search Tree Insert Operation Explanation and Binary Search Tree Delete Operation Explanation. Let’s look into the sample main function which utilizes Binary Search Tree class definition and functions defined above.
int main ()
{
BinarySearchTree<int>* root = new BinarySearchTree<int> (33);
insert_element_in_bst_recursive (20, root);
insert_element_in_bst_recursive (10, root);
insert_element_in_bst_recursive (30, root);
insert_element_in_bst_recursive (40, root);
insert_element_in_bst_recursive (50, root);
insert_element_in_bst_recursive (43, root);
insert_element_in_bst_recursive (77, root);
insert_element_in_bst_recursive (69, root);
insert_element_in_bst_recursive (25, root);
insert_element_in_bst_recursive (11, root);
insert_element_in_bst_recursive (10, root);
insert_element_in_bst_recursive (5, root);
insert_element_in_bst_recursive (18, root);
insert_element_in_bst_recursive (67, root);
insert_element_in_bst_recursive (88, root);
insert_element_in_bst_recursive (99, root);
insert_element_in_bst_recursive (65, root);
insert_element_in_bst_recursive (58, root);
insert_element_in_bst_recursive (51, root);
insert_element_in_bst_recursive (77, root);
print_tree (root);
search_element_in_bst_recursive (57, root);
search_element_in_bst_recursive (20, root);
search_element_in_bst_recursive (50, root);
BinarySearchTree<int>* min = find_minimum_element_in_bst_using_recursion (root);
BinarySearchTree<int>* max = find_maximum_element_in_bst_using_recursion (root);
cout << " Minimum element in BST: " << min -> m_data << endl;
cout << " Maximum element in BST: " << max -> m_data << endl;
int count = 0;
int k = 10;
BinarySearchTree<int>* k_max = find_kth_maximum_element_in_bst (root, k, &count);
cout << k << "th Maximum element in BST: " << k_max -> m_data << endl;
BinarySearchTree<int>* parent = NULL;
root = delete_element_in_bst_recursive (20, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (33, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (10, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (77, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (135, root, parent);
print_tree (root);
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 5 10 10 11 18 20 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 57 not found in BST !!!
Data: 20 found in BST !!!
Data: 50 found in BST !!!
Minimum element in BST: 5
Maximum element in BST: 99
10th Maximum element in BST: 50
Data: 20 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 33 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 10 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 77 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Data: 135 not found in BST !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99