A tree is a data structure similar to Linked list in which each node points to multiple nodes instead of simply pointing to the next node. A tree is called Binary tree if each node in a tree has maximum of two nodes.
An empty tree is also a Binary tree. We can call the two children of each node as Left and Right child of a node. The node of the tree which has no parent is called the Root of the tree. Perhaps Binary tree is the most used tree data structure in the programming world. Before going ahead have a look into Binary Tree basics, Binary Tree Traversal and Binary Tree implementation.
Let’s have a look on basic class definition for Binary Tree.
class BinaryTree
{
public:
int m_data;
BinaryTree* m_left;
BinaryTree* m_right;
BinaryTree (int data);
BinaryTree (int data, BinaryTree* left, BinaryTree* right);
~BinaryTree ();
};
void print_binary_tree (BinaryTree* root)
{
cout << " " << root -> m_data;
if (root -> m_left)
print_binary_tree (root -> m_left);
if (root -> m_right)
print_binary_tree (root -> m_right);
}
void print_tree (BinaryTree* root)
{
cout << "Binary tree contents: ";
print_binary_tree (root);
cout << endl;
}
Symmetric Tree
A binary tree is called symmetric tree if the root node’s left sub tree is the mirror image of right sub tree. Let’s have a look into below diagram to understand the symmetric tree.
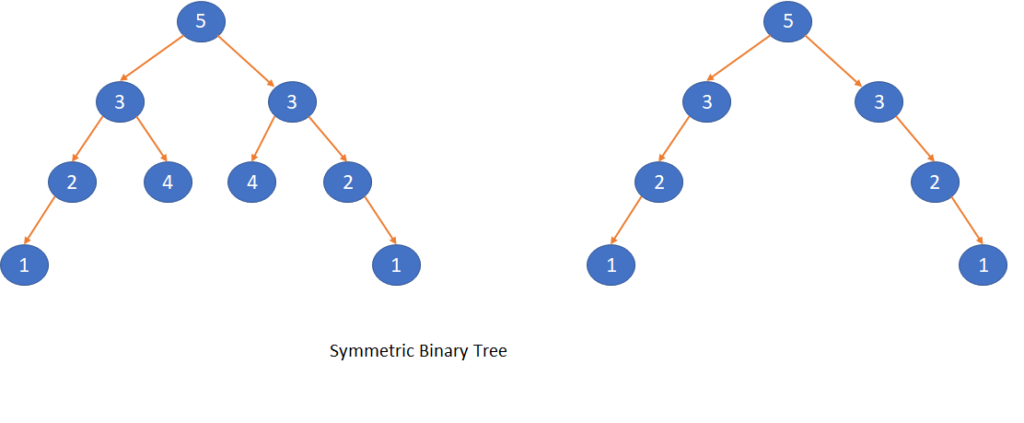
Algorithm
- If Tree is empty return True
- Call a recursive function and pass root node’s left child (L) and right child (R) as two arguments.
- If both arguments are not null and values are same then
- Call same recursive function with left’s child (L->right_child) and (R->left_child)
- Call same recursive function with left’s child (L->left_child) and (R->right_child)
- Else return false (if either of the argument’s value are not same)
Let’s look into the sample code to find out whether a binary tree is symmetric or not.
bool is_binary_tree_symmetric (BinaryTree* root1, BinaryTree* root2)
{
if (!root1 && !root2)
return true;
if (!root1 || !root2)
return false;
if (root1->m_data != root2->m_data)
return false;
return is_binary_tree_symmetric (root1->m_left, root2->m_right) &&
is_binary_tree_symmetric (root1->m_right, root2->m_left);
}
Few of the functions used below are explained in Binary Tree Implementation. Refer those before going ahead.
Let’s define a main function to use above functions.
int main ()
{
BinaryTree* node1 = new BinaryTree (1);
BinaryTree* node2 = new BinaryTree (2);
BinaryTree* node3 = new BinaryTree (3);
BinaryTree* node4 = new BinaryTree (4);
BinaryTree* node5 = new BinaryTree (5);
BinaryTree* node6 = new BinaryTree (1);
BinaryTree* node7 = new BinaryTree (2);
BinaryTree* node8 = new BinaryTree (3);
BinaryTree* node9 = new BinaryTree (4);
/* Set node5 as root node */
/*
5
3 3
2 4 4 2
1 1
*/
BinaryTree* root = node5;
node5 -> m_left = node3;
node3 -> m_left = node2;
node3 -> m_right = node4;
node2 -> m_left = node1;
node5 -> m_right = node8;
node8 -> m_right = node7;
node8 -> m_left = node9;
node7 -> m_right = node6;
print_tree (root);
cout << "Binary Tree is symmetric ? - " << is_binary_tree_symmetric (root, root) << endl;
}
Let’s look into the output of above function.
Binary tree contents: 5 3 2 1 4 3 4 2 1
Binary Tree is symmetric ? – 1