An AVL (Adelson-Velskii and Landis) Tree is a self balancing Binary Search Tree which has the following properties.
For any node “A”, the height of the left subtree of “A” and height of the right subtree of “A” differ by 1 at max.
In case of Binary search Trees worst case search complexity is O(n) in cases when the Binary Search Tree is skewed. In AVL tree, since heights of left and right subtree are balanced, hence search complexity improves to O(log n). Before going ahead have a look into Binary Search Tree basics, Binary Search Tree Insert, Binary Search Tree Delete, Binary Search Tree Search operations.
Let’s have a look into basic C++ class definition for Binary Search Tree.
template <typename T>
class BinarySearchTree
{
public:
T m_data;
BinarySearchTree* m_left;
BinarySearchTree* m_right;
BinarySearchTree (T data);
~BinarySearchTree ();
};
/* Below are some useful functions which we are going to use it in our examples */
template <typename T>
void print_binary_tree_inorder (BinarySearchTree<T>* root)
{
if (root -> m_left)
print_binary_tree_inorder (root -> m_left);
cout << " " << root -> m_data;
if (root -> m_right)
print_binary_tree_inorder (root -> m_right);
}
template <typename T>
void print_tree (BinarySearchTree<T>* root)
{
cout << "Binary tree contents: ";
print_binary_tree_inorder (root);
cout << endl;
}
/* Simply used this function to delete all nodes and free memory */
template <typename T>
void delete_all_nodes (BinarySearchTree<T>* root)
{
if (!root)
return;
if (root -> m_left)
{
delete_all_nodes (root -> m_left);
}
if (root -> m_right)
{
delete_all_nodes (root -> m_right);
}
delete root;
}
Checking if a Binary Search Tree is AVL Tree or not
In an AVL Tree, nodes are arranged in such a manner that height of left subtree and height of right subtree for every node differs by at max 1.
Algorithm
- Start from the root node.
- Calculate height of left subtree and right subtree.
- if difference is at max 1 then this node is balanced and repeat previous step for left and right child of the node.
- Repeat above 2 steps for every node in the tree if condition holds else break the loop if height is unbalanced for any node.
Let’s take an example to understand it better.
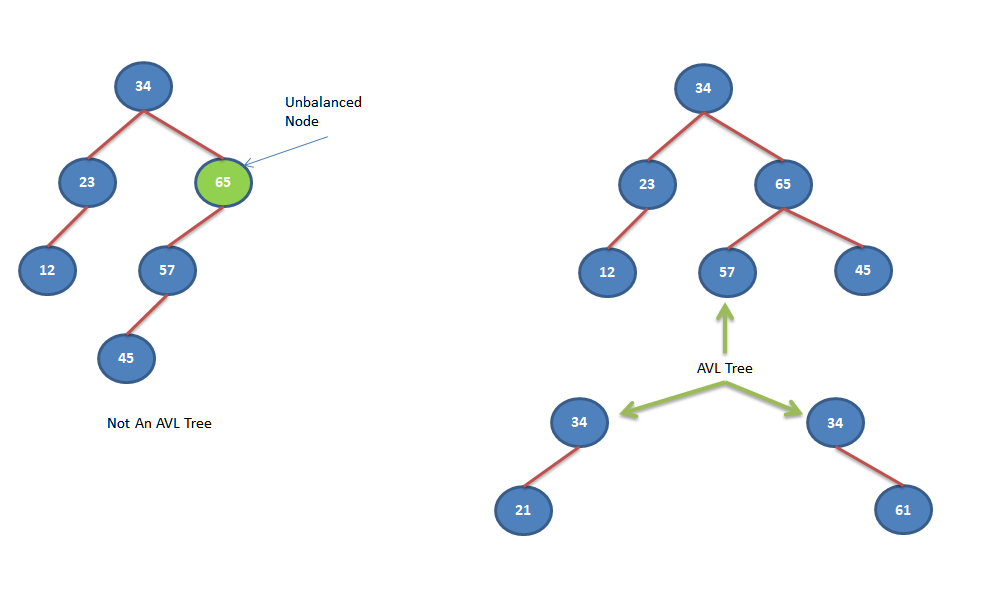
As shown in above diagram left side tree is unbalanced and hence not an AVL tree, while right side trees are balanced and hence an AVL Tree.
Let’s look into the sample code for this.
template <typename T>
int height_of_node (BinarySearchTree<T>* root)
{
if (!root)
return 0;
int left = height_of_node (root -> m_left);
int right = height_of_node (root -> m_right);
if (left > right)
return 1 + left;
else
return 1 + right;
}
template <typename T>
bool isAVL (BinarySearchTree<T>* root)
{
if (!root)
{
return true;
}
int left = height_of_node (root -> m_left);
int right = height_of_node (root -> m_right);
int diff = (left > right) ? left - right: right - left;
if (diff <= 1 && isAVL (root -> m_left) && isAVL (root -> m_right))
return true;
return false;
}
Few of the functions defined below are explained in Binary Search Tree Insert Operation Explanation and Binary Search Tree Delete Operation Explanation. Let’s look into the sample main function which utilizes Binary Search Tree class definition and functions defined above.
int main ()
{
BinarySearchTree<int>* root = new BinarySearchTree<int> (33);
insert_element_in_bst (20, root);
insert_element_in_bst (10, root);
insert_element_in_bst (30, root);
insert_element_in_bst (40, root);
insert_element_in_bst (50, root);
insert_element_in_bst (43, root);
insert_element_in_bst (77, root);
insert_element_in_bst (69, root);
insert_element_in_bst (25, root);
insert_element_in_bst (11, root);
insert_element_in_bst (10, root);
insert_element_in_bst (5, root);
insert_element_in_bst (18, root);
insert_element_in_bst (67, root);
insert_element_in_bst (88, root);
insert_element_in_bst (99, root);
insert_element_in_bst (65, root);
insert_element_in_bst (58, root);
insert_element_in_bst (51, root);
insert_element_in_bst (77, root);
print_tree (root);
cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;;
delete_all_nodes (root);
root = NULL;
root = new BinarySearchTree<int> (33);
insert_element_in_bst (20, root);
insert_element_in_bst (10, root);
insert_element_in_bst (77, root);
print_tree (root);
cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;;
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 5 10 10 11 18 20 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Binary Search Tree is AVL: 0
Binary tree contents: 10 20 33 77
Binary Search Tree is AVL: 1