A tree is a data structure similar to Linked list in which each node points to multiple nodes instead of simply pointing to the next node. A tree is called Binary tree if each node in a tree has maximum of two nodes.
An empty tree is also a Binary tree. We can call the two children of each node as Left and Right child of a node. The node of the tree which has no parent is called the Root of the tree. Perhaps Binary tree is the most used tree data structure in the programming world. Before going ahead have a look into Binary Tree basics, Binary Tree Traversal and Binary Tree implementation.
Let’s have a look on basic class definition for Binary Tree.
class BinaryTree
{
public:
int m_data;
BinaryTree* m_left;
BinaryTree* m_right;
BinaryTree (int data);
BinaryTree (int data, BinaryTree* left, BinaryTree* right);
~BinaryTree ();
};
void print_binary_tree (BinaryTree* root)
{
cout << " " << root -> m_data;
if (root -> m_left)
print_binary_tree (root -> m_left);
if (root -> m_right)
print_binary_tree (root -> m_right);
}
void print_tree (BinaryTree* root)
{
cout << "Binary tree contents: ";
print_binary_tree (root);
cout << endl;
}
SumTree
A SumTree is a Binary Tree where the value of a node is equal to the sum of the nodes present in its left subtree and right subtree. An empty tree is SumTree and the sum of an empty tree can be considered as 0. A leaf node is also considered as SumTree.
Let’s have a look into the below diagram to understand the Sum Tree.
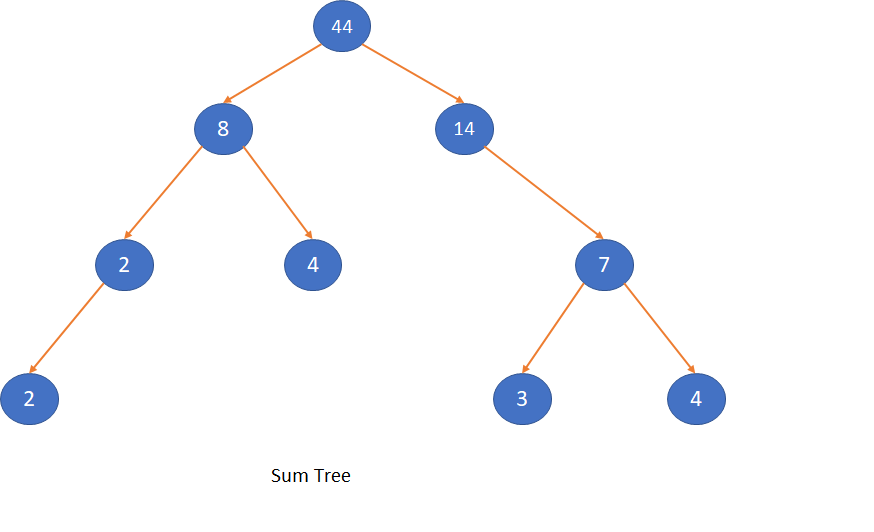
Algorithm
- If tree is empty, then return true as empty tree is a Sum Tree
- Call the recursive function with root node.
- Calculate the sum of left subtree and right subtree by passing respective node.
- If node doesn’t have any child then return the node value.
- If node has any child, then calculate the left and right sum of subtree by calling same function and return 2*node’s data.
- If sum of left subtree and right subtree is equal to root node then it’s a sum tree.
- Calculate the sum of left subtree and right subtree by passing respective node.
Let’s look into the sample code to check whether a binary tree is sum tree or not.
int is_binary_tree_sum_tree_helper (BinaryTree* root)
{
if (!root)
return 0;
if (!root->m_right && !root->m_left)
return root->m_data;
int right = is_binary_tree_sum_tree_helper (root->m_right);
int left = is_binary_tree_sum_tree_helper (root->m_left);
if (root->m_data == (right + left))
return root->m_data * 2;
return -1;
}
bool is_binary_tree_sum_tree (BinaryTree* root)
{
if (!root)
return true;
int right = is_binary_tree_sum_tree_helper (root->m_right);
int left = is_binary_tree_sum_tree_helper (root->m_left);
if (root->m_data == (right + left))
return true;
return false;
}
Few of the functions used below are explained in Binary Tree Implementation. Refer those before going ahead.
Let’s define a main function to use above functions.
int main ()
{
BinaryTree* node1 = new BinaryTree (1);
BinaryTree* node2 = new BinaryTree (1);
BinaryTree* node3 = new BinaryTree (6);
BinaryTree* node4 = new BinaryTree (4);
BinaryTree* node5 = new BinaryTree (24);
BinaryTree* node6 = new BinaryTree (1);
BinaryTree* node7 = new BinaryTree (1);
BinaryTree* node8 = new BinaryTree (6);
BinaryTree* node9 = new BinaryTree (4);
/* Set node5 as root node */
/*
24
6 6
1 4 4 1
1 1
*/
BinaryTree* root = node5;
node5 -> m_left = node3;
node3 -> m_left = node2;
node3 -> m_right = node4;
node2 -> m_left = node1;
node5 -> m_right = node8;
node8 -> m_right = node7;
node8 -> m_left = node9;
node7 -> m_right = node6;
print_tree (root);
cout << "Binary Tree is sum tree ? - " << is_binary_tree_sum_tree (root) << endl;
}
Let’s look into the output of the above function.
Binary tree contents: 24 6 1 1 4 6 4 1 1
Binary Tree is sum tree ? - 1