A Maximum Heap is a binary tree which has following properties:
- Binary tree MUST be a complete binary tree which means all leaf nodes are present in either at height “h” or “h-1”.
- Key stored in each node is smaller than or equal to keys in the node’s children.
Before going ahead, have a look into Binary Tree.
Below are some examples of Maximum Heap.
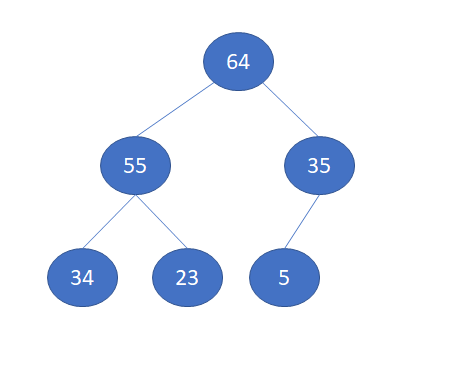
Maximum Heap Implementation
Let’s have a look into Maximum Heap Implementation.
Maximum Heap Class Implementation
Let’s have a look into the basic class definition of Maximum Heap Class.
#define MAX_PRIORITY_QUEUE_SIZE 10
class MaxHeap
{
private:
int m_size;
int m_data[MAX_PRIORITY_QUEUE_SIZE];
int get_parent (int child_node_id);
int left_child (int parent_id);
int right_child (int parent_id);
public:
MaxHeap ();
int get_size ();
void insert (int data);
bool isEmpty ();
int find_maximum ();
int delete_maximum ();
void percolate_down (int hole);
void percolate_up (int hole);
void print_content ()
{
for (int i = 0; i < m_size; i++)
{
std::cout << m_data[i] << " ";
}
std::cout << std::endl;
}
};
Let’s look into some of the Helper functions of Maximum Heap Class.
MaxHeap::MaxHeap (): m_size(0)
{}
int MaxHeap::get_size ()
{
return m_size;
}
int MaxHeap::get_parent (int child_node_id)
{
if (child_node_id <= 0 || child_node_id >= m_size)
return -1;
return (child_node_id - 1)/2;
}
int MaxHeap::left_child (int parent_id)
{
int left = 2 * parent_id + 1;
if (left >= m_size)
return -1;
return left;
}
int MaxHeap::right_child (int parent_id)
{
int right = 2 * parent_id + 2;
if (right >= m_size)
return -1;
return right;
}
bool MaxHeap::isEmpty ()
{
return (m_size == 0);
}
int MaxHeap::find_maximum ()
{
return m_data[0];
}
Inserting an element in Maximum Heap Class
Algorithm
To insert an element X in the Heap
- First the element X is put in at the last place (as a leaf node) in the binary tree.
- Now, we need to find the correct place of this new node so that Heap property is satisfied.
- Element X is compared with its parent node,
- if parent is smaller then nodes are swapped.
- else element X is at correct location and heap property is satisfied.
- Repeat the above step until we reach the root node or no swapping is done.
The Strategy followed to insert the node is called Percolate up.
Let’s understand inserting an element in Maximum Heap through some examples.
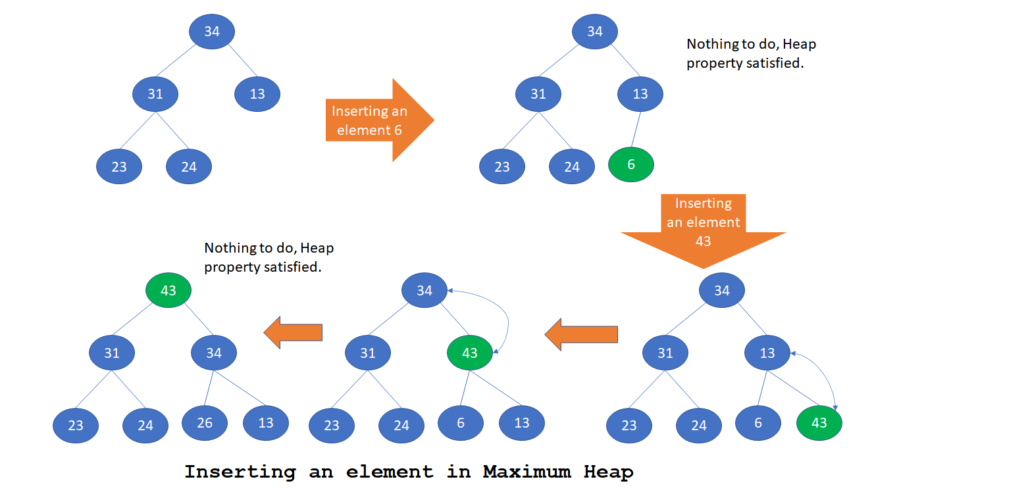
Let’s have a look at the sample function to perform insertion of an element in Maximum Heap.
void MaxHeap::insert (int data)
{
int hole = m_size++;
m_data[hole] = data;
percolate_up (hole);
}
void MaxHeap::percolate_up (int hole)
{
int parent = get_parent (hole);
if (parent == -1)
return;
if (m_data[parent] < m_data[hole])
{
int temp = m_data[parent];
m_data[parent] = m_data[hole];
m_data[hole] = temp;
percolate_up (parent);
}
}
Deleting an element in Maximum Heap
Algorithm
Deletion in a heap always happens of the root node. In case of Maximum heap, maximum node value will be deleted always. In order to delete maximum element node X in a maximum heap.
- Delete the root node. After this step, heap property needs to be established again.
- Put the last element node (say Y) at the root.
- Compare the root node value (Y) to its children.
- If root node value is lower than its child having maximum value, then swap the nodes.
- Else Heap property is established.
- If any swapping of nodes is done in previous step, then repeat above step at the new position of node Y.
The strategy followed to deleting the minimum node is called Percolate Down.
Let’s understand deleting maximum element in Maximum Heap through some examples.
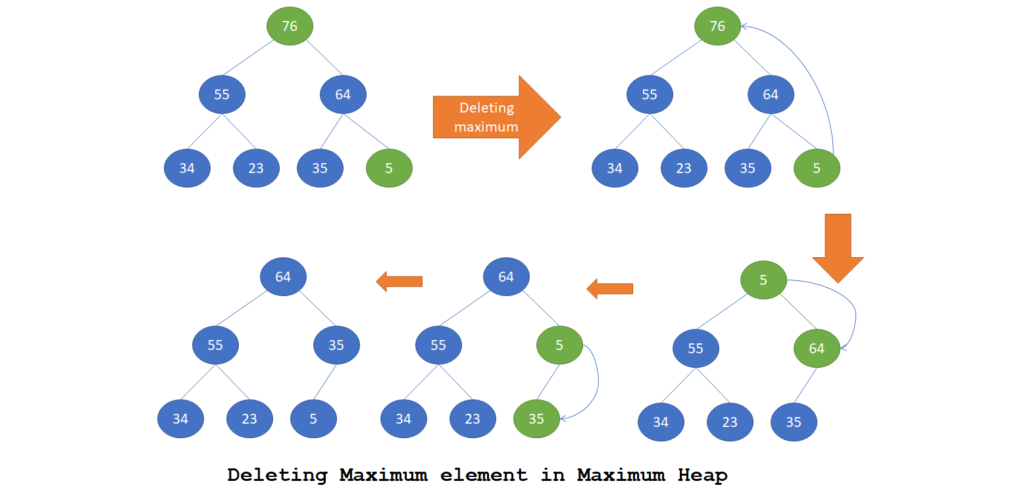
Let’s have a look at the sample function to perform deletion of maximum element in Maximum Heap.
int MaxHeap::delete_maximum ()
{
int min_val = m_data[0];
m_data[0] = m_data[--m_size];
percolate_down (0);
return min_val;
}
void MaxHeap::percolate_down (int hole)
{
int left = left_child (hole);
int right = right_child (hole);
int min = hole;
if (left != -1 && m_data[left] > m_data[min])
min = left;
if (right != -1 && m_data[right] > m_data[min])
min = right;
if (min != hole)
{
int temp = m_data[min];
m_data[min] = m_data[hole];
m_data[hole] = temp;
percolate_down (min);
}
}
Let’s have a look at the sample function which utilizes above Maximum heap class functions.
void testMaxHeap ()
{
MaxHeap q;
q.print_content ();
q.insert (30);
q.print_content ();
q.insert (50);
q.print_content ();
q.insert (10);
q.print_content ();
q.insert (60);
q.print_content ();
q.insert (3);
q.print_content ();
while (!q.isEmpty ())
{
cout << "Maximum value: " << q.find_maximum () << " Size: " << q.get_size () << endl;
q.delete_maximum ();
}
}
Let’s analyze the output of above main function.
30
50 30
50 30 10
60 50 10 30
60 50 10 30 3
Maximum value: 60 Size: 5
Maximum value: 50 Size: 4
Maximum value: 30 Size: 3
Maximum value: 10 Size: 2
Maximum value: 3 Size: 1