A Binary Search Tree is a Binary tree in which all the nodes has following properties.
- Left subtree of a node contains all the nodes having values lesser than the node.
- Right subtree of a node contains all the nodes having values higher than the node.
- Both the left and right subtree is also a Binary Search Tree.
As the name suggests, this data structure is mainly used for faster searching. In order to do that, restrictions are applied while inserting/deleting an element into the tree. As a result of these restrictions, worst case search time complexity remains at O(log n). Before going ahead have a look into Binary Search Tree basics, Binary Search Tree Insert, Binary Search Tree Delete, Binary Search Tree Search operations.
Let’s have a look into basic C++ class definition for Binary Search Tree.
template <typename T>
class BinarySearchTree
{
public:
T m_data;
BinarySearchTree* m_left;
BinarySearchTree* m_right;
BinarySearchTree (T data);
~BinarySearchTree ();
};
/* Below are some useful functions which we are going to use it in our examples */
template <typename T>
void print_binary_tree_inorder (BinarySearchTree<T>* root)
{
if (root -> m_left)
print_binary_tree_inorder (root -> m_left);
cout << " " << root -> m_data;
if (root -> m_right)
print_binary_tree_inorder (root -> m_right);
}
template <typename T>
void print_tree (BinarySearchTree<T>* root)
{
cout << "Binary tree contents: ";
print_binary_tree_inorder (root);
cout << endl;
}
/* Simply used this function to delete all nodes and free memory */
template <typename T>
void delete_all_nodes (BinarySearchTree<T>* root)
{
if (!root)
return;
if (root -> m_left)
{
delete_all_nodes (root -> m_left);
}
if (root -> m_right)
{
delete_all_nodes (root -> m_right);
}
delete root;
}
Finding Minimum value in Binary Search Tree
In Binary Search Tree data is stored in a particular manner due to which inorder traversal of Binary Search Tree will provide a sorted list. Based on the property of Binary Search Tree in which left node is lower than root node which is lower than right node, we can establish that left most child of the Binary Search Tree is the node having minimum value in Binary Search Tree.
Algorithm
- Start from the root and repeat below step.
- If left child is present then go to left child else current node is the minimum value node.
Let’s take an example to understand the working of above algorithm to find out the node with minimum value.
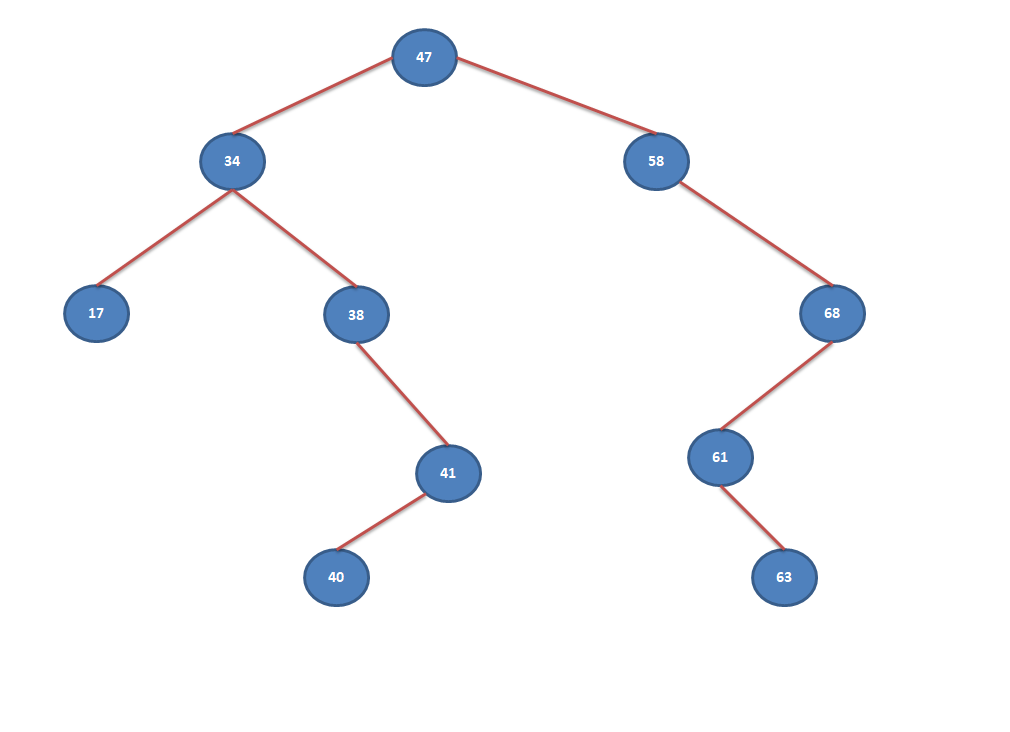
- Start with the root element “47”.
- Node “47” has left child “34”, so move towards it.
- Node “34” has left child “17”, so move towards it.
- Node “17” has no left child. Hence this is the node with minimum value.
This operation can be implemented in both iterative and recursive manner.
Finding Minimum value in Binary Search Tree using iterative method
Let’s look into the sample code.
template <typename T>
BinarySearchTree<T>* find_minimum_element_in_bst_using_iteration (BinarySearchTree<T>* root)
{
if (!root)
{
cout << "BST tree is empty !!!" << endl;
return NULL;
}
BinarySearchTree<T>* temp = root;
while (temp)
{
if (temp -> m_left)
{
temp = temp -> m_left;
}
else
{
return temp;
}
}
}
Finding Minimum value in Binary Search Tree using recursive method
Let’s look into the sample code.
template <typename T>
BinarySearchTree<T>* find_minimum_element_in_bst_using_recursion (BinarySearchTree<T>* root)
{
if (!root)
{
cout << "BST tree is empty !!!" << endl;
return NULL;
}
if (root -> m_left)
{
return find_minimum_element_in_bst_using_recursion (root -> m_left);
}
else
{
return root;
}
}
Few of the functions defined below are explained in Binary Search Tree Insert Operation Explanation and Binary Search Tree Delete Operation Explanation.
Let’s look into the sample main function which utilizes Binary Search Tree class definition and iterative functions defined above.
int main ()
{
BinarySearchTree<int>* root = new BinarySearchTree<int> (33);
insert_element_in_bst (20, root);
insert_element_in_bst (10, root);
insert_element_in_bst (30, root);
insert_element_in_bst (40, root);
insert_element_in_bst (50, root);
insert_element_in_bst (43, root);
insert_element_in_bst (77, root);
insert_element_in_bst (69, root);
insert_element_in_bst (25, root);
insert_element_in_bst (11, root);
insert_element_in_bst (10, root);
insert_element_in_bst (5, root);
insert_element_in_bst (18, root);
insert_element_in_bst (67, root);
insert_element_in_bst (88, root);
insert_element_in_bst (99, root);
insert_element_in_bst (65, root);
insert_element_in_bst (58, root);
insert_element_in_bst (51, root);
insert_element_in_bst (77, root);
print_tree (root);
BinarySearchTree<int>* min = find_minimum_element_in_bst_using_iteration (root);
BinarySearchTree<int>* max = find_maximum_element_in_bst_using_iteration (root);
cout << " Minimum element in BST: " << min -> m_data << endl;
cout << " Maximum element in BST: " << max -> m_data << endl;
root = delete_element_in_bst (20, root);
print_tree (root);
root = delete_element_in_bst (33, root);
print_tree (root);
root = delete_element_in_bst (10, root);
print_tree (root);
root = delete_element_in_bst (77, root);
print_tree (root);
root = delete_element_in_bst (135, root);
print_tree (root);
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 5 10 10 11 18 20 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Minimum element in BST: 5
Maximum element in BST: 99
Data: 20 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 33 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 10 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 77 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Data: 135 not found in BST !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Few of the functions defined below are explained in Binary Search Tree Insert Operation Explanation and Binary Search Tree Delete Operation Explanation.
Let’s look into the sample main function which utilizes Binary Search Tree class definition and recursive functions defined above.
int main ()
{
BinarySearchTree<int>* root = new BinarySearchTree<int> (33);
insert_element_in_bst_recursive (20, root);
insert_element_in_bst_recursive (10, root);
insert_element_in_bst_recursive (30, root);
insert_element_in_bst_recursive (40, root);
insert_element_in_bst_recursive (50, root);
insert_element_in_bst_recursive (43, root);
insert_element_in_bst_recursive (77, root);
insert_element_in_bst_recursive (69, root);
insert_element_in_bst_recursive (25, root);
insert_element_in_bst_recursive (11, root);
insert_element_in_bst_recursive (10, root);
insert_element_in_bst_recursive (5, root);
insert_element_in_bst_recursive (18, root);
insert_element_in_bst_recursive (67, root);
insert_element_in_bst_recursive (88, root);
insert_element_in_bst_recursive (99, root);
insert_element_in_bst_recursive (65, root);
insert_element_in_bst_recursive (58, root);
insert_element_in_bst_recursive (51, root);
insert_element_in_bst_recursive (77, root);
print_tree (root);
BinarySearchTree<int>* min = find_minimum_element_in_bst_using_recursion (root);
BinarySearchTree<int>* max = find_maximum_element_in_bst_using_recursion (root);
cout << " Minimum element in BST: " << min -> m_data << endl;
cout << " Maximum element in BST: " << max -> m_data << endl;
BinarySearchTree<int>* parent = NULL;
root = delete_element_in_bst_recursive (20, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (33, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (10, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (77, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (135, root, parent);
print_tree (root);
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 5 10 10 11 18 20 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Minimum element in BST: 5
Maximum element in BST: 99
Data: 20 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 33 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 10 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 77 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Data: 135 not found in BST !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99