Construct A Binary Tree From Inorder and Postorder Traversal

A tree is a data structure similar to Linked list in which each node points to multiple nodes instead of simply pointing to the next node. A tree is called Binary tree if each node in a tree has maximum of two nodes.
An empty tree is also a Binary tree. We can call the two children of each node as Left and Right child of a node. The node of the tree which has no parent is called the Root of the tree. Perhaps Binary tree is the most used tree data structure in the programming world. Before going ahead have a look into Binary Tree basics, Binary Tree Traversal and Binary Tree implementation.

Let’s have a look on basic class definition for Binary Tree.

class BinaryTree
{
    public:
        int m_data;
        BinaryTree* m_left;
        BinaryTree* m_right;
        BinaryTree (int data);
        BinaryTree (int data, BinaryTree* left, BinaryTree* right);
        ~BinaryTree ();
};

void print_binary_tree (BinaryTree* root)
{
    cout << " " << root -> m_data;
    if (root -> m_left)
        print_binary_tree (root -> m_left);
    if (root -> m_right)
        print_binary_tree (root -> m_right);
}

void print_tree (BinaryTree* root)
{
    cout << "Binary tree contents: ";
    print_binary_tree (root);
    cout << endl;
}

Construct Binary Tree from Postorder and Inorder traversal

Before going ahead let’s look into the definition of Postorder and Inorder Traversal.

• Inorder Traversal — In Inorder Traversal root node is visited in between it’s left and right child.
• Postorder Traversal — In Postorder Traversal root node is visited after it’s left and right child.

Important Points

• In Postorder traversal sequence, rightmost element is the root of the binary tree.
• In Inorder traversal sequence, all the nodes present in left side of any element is in left subtree of that node where as right side elements are on the right subtree.

Let’s look into a sample Binary Tree.

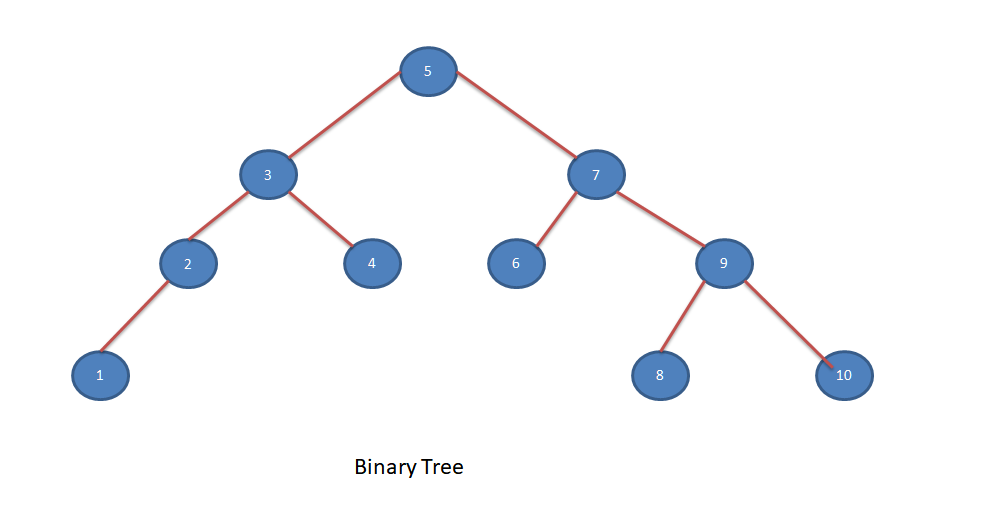
Postorder traversal of above Binary Tree: 1, 2, 4, 3, 6, 8, 10, 9, 7, 5
Inorder traversal of above Binary Tree: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

In this article we will define a function which will take above traversal as an argument and create the Binary Tree shown in above diagram.
Let’s look into the algorithm to construct the binary tree.

Algorithm

• Select first element from Postorder list and increment the postorder index.
• Create a Binary tree node (new_node) and set the value as selected postorder list value.
• Find the selected element index(inorder_index) in Inorder list.
• Call recursive function again with right side of inorder_index items in inorder list and set as the right child of new_node.
• Call recursive function again with left side of inorder_index items in inorder list and set as the left child of new_node.
• return new_node

Few of the functions used below are explained in Binary Tree Implementation. Refer those before going ahead.
Let’s look into the sample function.

BinaryTree* construct_binary_tree (int inorder[], int postorder[], int length, int inorder_index_start, int inorder_index_end)
{
    static int postorder_index = length - 1;
    if (inorder_index_start > inorder_index_end)
        return NULL;
    BinaryTree* newNode = new BinaryTree(postorder[postorder_index]);

    postorder_index--;
    /* All node Processed */
    if (inorder_index_end == inorder_index_start)
        return newNode;

    /* find above node place in inorder list */
    int index = 0;
    for (int i = 0; i < length; i++)
    {
        if (inorder[i] == newNode -> m_data)
        {
            index = i;
            break;
        }
    }

    /* Inorder list items present in left side of index is in left subtree while rest of them are in right subtree */
    newNode -> m_right = construct_binary_tree (inorder, postorder, length, index + 1, inorder_index_end);
    newNode -> m_left = construct_binary_tree (inorder, postorder, length, inorder_index_start, index - 1);
    return newNode;
}

Let’s define a main function which will use above function to create Binary tree.

int main ()
{
    int postorder[] = {1, 2, 4, 3, 6, 8, 10, 9, 7, 5};
    int inorder[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
    BinaryTree* root = construct_binary_tree (inorder, postorder, 10, 0, 9);
    print_tree (root);
}

Let’s analyze the output of above main function.

Binary tree contents:  5 3 2 1 4 7 6 9 8 10