Graph is a data structure which consists of a set of vertices which is called as Node, together with a set of collection of pair of vertices which is called as an Edge.
A graph data structure can be represented as a pair (V, E) where V is a set of nodes called vertices and E is a collection of pairs of vertices called edges. Graphs are used to solve many real-life problems such as fastest ways to go from A to B etc.
A Graph is called connected graph if each of the vertices of the graph is connected from each of the other vertices which means there is a path available from any vertex to any other vertex in the Graph.
Before going ahead have a look into Graph Basics.
Let’s have a look at the example of connected Graph.
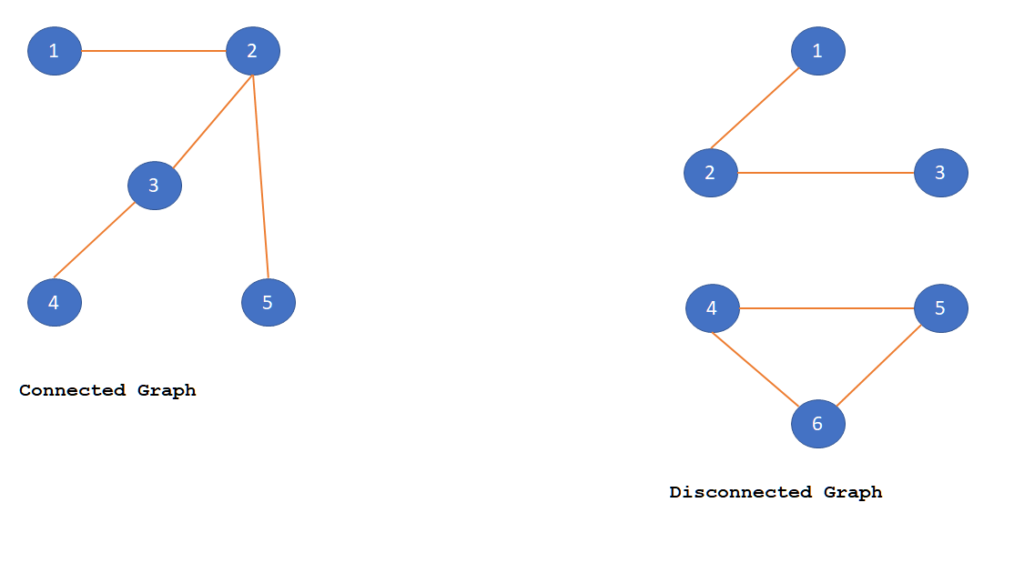
Algorithm
A graph is connected or not can be find out using Depth First Search traversal method. Let’s have a look at the algorithm to find a connected graph.
- Pick any graph node to start the traversal and push it into a Stack.
- Pop the topmost item of the Stack, marked it as visited.
- Push all the non-visited neighboring nodes of the popped node into the Stack.
- Keep repeating Steps 2 and 3 until all Graph nodes are visited.
- If there is a vertex which is still unvisited then graph is called disconnected else, it is a connected graph.
Let’s have a look at the class definition and member function definition of a Graph class.
class Graph
{
private:
int m_nodes;
int m_edges;
int **edges;
bool isUndirected;
int isConnected;
public:
Graph (int nodes, bool isUndirected);
int getNumberOfNodes ();
int getNumberOfEdges ();
void getEdges ();
bool addEdge (int srcNode, int dstNode);
void BFS (int start);
void DFS (int start);
~Graph ();
bool isConnectedGraph ();
bool printMotherVertex ();
void topologicalSort ();
void getEdgesIn2DFormat ();
};
Graph::~Graph ()
{
if (!edges)
{
cout << "Graph was never initializaed, nothing to free " << endl;
return;
}
for (int i = 0; i < m_nodes; i++)
{
delete [] edges[i];
}
delete [] edges;
}
Graph::Graph (int nodes, bool isUndirected): m_nodes (nodes),
m_edges (0),
edges (NULL),
isUndirected (isUndirected),
isConnected (-1)
{
edges = new int*[m_nodes];
if (!edges)
{
cout << "Graph initialization failed " << endl;
}
for (int i = 0; i < m_nodes; i++)
{
edges[i] = new int[m_nodes];
}
for (int i = 0; i < m_edges; i++)
{
for (int j = 0; j < m_edges; j++)
{
edges[i][j] = 0;
}
}
}
int Graph::getNumberOfNodes ()
{
return m_nodes;
}
int Graph::getNumberOfEdges ()
{
return m_edges;
}
void Graph::getEdges ()
{
if (!edges)
{
cout << "Graph is not initialized properly " << endl;
}
for (int i = 0; i < m_nodes; i++)
{
for (int j = 0; j < m_nodes; j++)
{
cout << "Node " << i << " and Node " << j << " edge status: " << edges[i][j] << endl;
}
}
}
bool Graph::addEdge (int srcNode, int dstNode)
{
if (srcNode >= m_nodes || dstNode >= m_nodes)
{
cout << "srcNode " << srcNode << " or dstNode " << dstNode << " is out of known max node: " << m_nodes << endl;
return false;
}
if (edges[srcNode][dstNode])
{
cout << "srcNode " << srcNode << " or dstNode " << dstNode << " is already existed." << endl;
return false;
}
edges[srcNode][dstNode] = 1;
++m_edges;
if (isUndirected)
{
edges[dstNode][srcNode] = 1;
++m_edges;
}
return true;
}
void Graph::getEdgesIn2DFormat ()
{
cout << "Printing edges in 2D format!!" << endl;
for (int i = 0; i < m_nodes; i++)
{
for (int j = 0; j < m_nodes; j++)
{
cout << edges[i][j] << " ";
}
cout << endl;
}
}
Before going ahead, let’s have a look at Stack and Its implementation for better understanding.
Let’s have a look at the modified Depth First Traversal function to check whether a graph is connected or not.
void Graph::DFS (int start)
{
cout << "Starting DFS traversing of Graph from Node: " << start << endl;
bool visited[m_nodes] = {false};
if (m_nodes == 0)
{
cout << "There is no nodes present in Graph" << endl;
}
if (start < 0)
{
start = 0;
}
if (start >= m_nodes)
{
cout << "Graph traversal not possible as start node not found" << endl;
return;
}
Stack s(m_nodes);
s.push (start);
while (!s.isEmpty ())
{
int visiting = s.pop ();
if (visited[visiting])
{
cout << "Graph node " << visiting << " Already visited, skipping!!!" << endl;
continue;
}
visited[visiting] = true;
cout << "Visited node: " << visiting << " in the Graph." << endl;
for (int i = 0; i < m_nodes; i++)
{
if (edges[visiting][i] && !visited[i])
{
cout << "Pushing node " << i << endl;
s.push (i);
}
}
}
/* Below code is to check whether Graph is connected or not */
isConnected = -1;
for (int i = 0; i < m_nodes; i++)
{
if (!visited[i])
{
isConnected = 0;
break;
}
}
if (isConnected == -1)
{
isConnected = 1;
}
}
bool Graph::isConnectedGraph ()
{
if (isConnected == -1)
{
DFS (0);
}
return isConnected;
}
Let’s have a look at the main function which utilizes above functions.
void add_header (const char *line)
{
cout << "========================================================================" << endl;
cout << line << endl;
cout << "========================================================================" << endl;
}
int main ()
{
Graph g(5, true);
g.addEdge (1,2);
g.addEdge (0,2);
g.addEdge (3,2);
g.addEdge (4,2);
g.addEdge (1,3);
g.addEdge (1,4);
g.addEdge (1,5);
g.addEdge (1,7);
g.addEdge (1,0);
g.addEdge (2,2);
g.addEdge (3,2);
g.addEdge (4,2);
g.addEdge (5,2);
cout << "Graph has nodes: " << g.getNumberOfNodes () << endl;
cout << "Graph has edges: " << g.getNumberOfEdges () << endl;
add_header ("Printing Edges information in Adjecency Matrix Format.");
g.getEdgesIn2DFormat ();
add_header ("Printing DFS traversal of Graph");
g.DFS (0);
add_header ("Checking Graph Connected Status");
cout << "Graph connected status: " << g.isConnectedGraph () << endl;
}
Let’s analyze the output of above main function.
srcNode 1 or dstNode 5 is out of known max node: 5
srcNode 1 or dstNode 7 is out of known max node: 5
srcNode 3 or dstNode 2 is already existed.
srcNode 4 or dstNode 2 is already existed.
srcNode 5 or dstNode 2 is out of known max node: 5
Graph has nodes: 5
Graph has edges: 16
========================================================================
Printing Edges information in Adjecency Matrix Format.
========================================================================
Printing edges in 2D format!!
0 1 1 0 0
1 0 1 1 1
1 1 1 1 1
0 1 1 0 0
0 1 1 0 0
========================================================================
Printing DFS traversal of Graph
========================================================================
Starting DFS traversing of Graph from Node: 0
Visited node: 0 in the Graph.
Pushing node 1
Pushing node 2
Visited node: 2 in the Graph.
Pushing node 1
Pushing node 3
Pushing node 4
Visited node: 4 in the Graph.
Pushing node 1
Visited node: 1 in the Graph.
Pushing node 3
Visited node: 3 in the Graph.
Graph node 3 Already visited, skipping!!!
Graph node 1 Already visited, skipping!!!
Graph node 1 Already visited, skipping!!!
========================================================================
Checking Graph Connected Status
========================================================================
Graph connected status: 1