Breadth first search for a Graph

Traversal of a Graph means visiting each and every nodes present in the Graph. Traversal can be done using various approaches and here we are going to talk about one of most famous and useful traversal algorithm known as Breadth first search (BFS). In this algorithm, backtracking and recursion is being used along with a Queue to visit all the nodes. Before going ahead have a look into Graph Basics.

Breadth first search (BFS) algorithm

The idea of this algorithm is to visit all the nodes of the graph avoiding any cycles. To do this we are going to need following items:

• Queue
• Backtracking
• Recursion

BFS algorithm steps

• Pick any graph node to start the traversal and Enqueue it into a Queue.
• Dequeue the node from the Queue, marked it as visited.
• Enqueue all the non visited neighbouring nodes of the Dequeued node into the Queue.
• Keep repeating Steps 2 and 3 until all Graph nodes are visited.

Let’s take an example to understand clearly how this algorithm works.
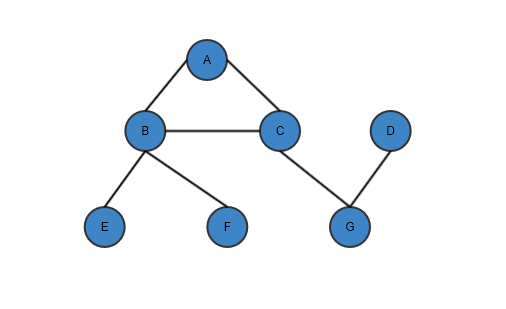
Below is the sample Graph which we are going to traverse using BFS algorithm.

Now, let’s see how BFS actually works step by step.
We are going to start traversal from Node A.

Enqueue A into Queue. Queue contains -- A, Visited Node -- 0
Dequeue node A from Queue and mark it visited. Queue contains -- 0, Visited Node -- A
Enqueue all unvisited neighbouring nodes of A to Queue. Queue contains -- B, C. Visited Node -- A
Dequeue Node B from Queue and mark it visited. Queue contains -- C. Visited Node -- A, B
Enqueue all unvisited neighbouring nodes of B to Queue. Queue contains -- C, E, F. Visited Node -- A, B
Dequeue Node C from Queue and mark it visited. Queue contains -- E, F. Visited Node -- A, B, C
Enqueue all unvisited neighbouring nodes of C to Queue. Queue contains -- E, F, G. Visited Node -- A, B, C
Dequeue Node E from Queue and mark it visited. Queue contains -- F, G. Visited Node -- A, B, C, E
Enqueue all unvisited neighbouring nodes of E to Queue. Queue contains -- F, G. Visited Node -- A, B, C, E
Dequeue Node F from Queue and mark it visited. Queue contains -- G. Visited Node -- A, B, C, E, F
Enqueue all unvisited neighbouring nodes of F to Queue. Queue contains -- G. Visited Node -- A, B, C, E, F
Dequeue Node G from Queue and mark it visited. Queue contains -- 0. Visited Node -- A, B, C, E, F, G
Enqueue all unvisited neighbouring nodes of G to Queue. Queue contains -- D. Visited Node -- A, B, C, E, F, G
Dequeue Node D from Queue and mark it visited. Queue contains -- 0. Visited Node -- A, B, C, E, F, G, D
Enqueue all unvisited neighbouring nodes of D to Queue. Queue contains -- 0. Visited Node -- A, B, C, E, F, G, D
Traversal is complete as Queue is empty now.

Let’s have a look into implementation code. Check Graph and its basic implementation before going ahead.

class Graph
{
    private:
        int m_nodes;
        int m_edges;
        int **edges;
        bool isUndirected;
 
    public:
        Graph (int nodes, bool isUndirected);
        int getNumberOfNodes ();
        int getNumberOfEdges ();
        void getEdges ();
        bool addEdge (int srcNode, int dstNode);
        void BFS (int start);
        ~Graph ();
};

void Graph::BFS (int start)
{
    cout << "Starting BFS traversing of Graph from Node: " << start << endl;
    bool visited[m_nodes] = {false};

    if (m_nodes == 0)
    {
        cout << "There is no nodes present in Graph" << endl;
    }

    if (start < 0)
    {
        start = 0;
    }

    if (start >= m_nodes)
    {
        cout << "Graph traversal not possible as start node not found" << endl;
        return;
    }

    Queue q(m_nodes);
    q.enqueue (start);

    while (!q.isEmpty ())
    {
        int visiting = q.dequeue ();

        if (visited[visiting])
        {
            cout << "Graph node " << visiting << " Already visited, skipping!!!" << endl;
            continue;
        }

        visited[visiting] = true;

        cout << "Visited node: " << visiting << " in the Graph." << endl;
        for (int i = 0; i < m_nodes; i++)
        {
            if (edges[visiting][i] && !visited[i])
            {
                cout << "Pushing node " << i << endl;
                q.enqueue (i);
            }
        }
    }
}

Let’s define a sample Graph and check how this code works.

int main ()
{
    Graph g(5, true);
    g.addEdge (1,2);
    g.addEdge (0,2);
    g.addEdge (3,2);
    g.addEdge (4,2);
    g.addEdge (1,3);
    g.addEdge (1,4);
    g.addEdge (1,5);
    g.addEdge (1,7);
    g.addEdge (1,0);
    g.addEdge (2,2);
    g.addEdge (3,2);
    g.addEdge (4,2);
    g.addEdge (5,2);
    cout << "Graph has nodes: " << g.getNumberOfNodes () << endl;
    cout << "Graph has edges: " << g.getNumberOfEdges () << endl;
    g.BFS (0);
}

Let’s check the output of above code.

Starting BFS traversing of Graph from Node: 4
Visited node: 4 in the Graph.
Pushing node 1
Pushing node 2
Visited node: 1 in the Graph.
Pushing node 0
Pushing node 2
Pushing node 3
Visited node: 2 in the Graph.
Pushing node 0
Pushing node 3
Visited node: 0 in the Graph.
Graph node 2 Already visited, skipping!!!
Visited node: 3 in the Graph.
Graph node 0 Already visited, skipping!!!
Graph node 3 Already visited, skipping!!!

Time Complexity: O(V^2)

Applications of BFS

• Finding all connected components and neighbour nodes
• Shortest path between two nodes
• Checking a graph for bipartiness