A tree is a data structure similar to Linked list in which each node points to multiple nodes instead of simply pointing to the next node. A tree is called Binary tree if each node in a tree has maximum of two nodes.
Boundary traversal of a binary tree, traverses through all the boundary nodes which includes
- The left boundary of a binary tree
- All the leaves of the binary tree
- The right boundary of a binary tree
Before going ahead have a look into Binary Tree basics, Binary Tree Traversal and Binary Tree implementation.
Let’s have a look on basic class definition for Binary Tree.
class BinaryTree
{
public:
int m_data;
BinaryTree* m_left;
BinaryTree* m_right;
BinaryTree (int data);
BinaryTree (int data, BinaryTree* left, BinaryTree* right);
~BinaryTree ();
};
void print_binary_tree (BinaryTree* root)
{
cout << " " << root -> m_data;
if (root -> m_left)
print_binary_tree (root -> m_left);
if (root -> m_right)
print_binary_tree (root -> m_right);
}
void print_tree (BinaryTree* root)
{
cout << "Binary tree contents: ";
print_binary_tree (root);
cout << endl;
}
Boundary Traversal
Boundary traversal of a binary tree, traverses through all the boundary nodes which includes
- The left boundary of a binary tree
- All the leaves of the binary tree
- The right boundary of a binary tree
Let’s have a look into below diagram to understand how boundary traversal works.
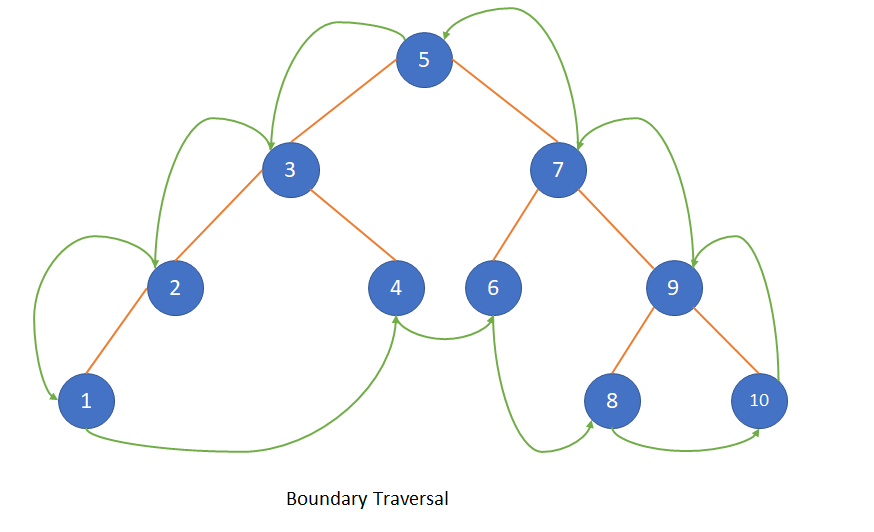
Boundary traversal of above tree is 5,3,2,1,4,6,8,10,9,7
Algorithm
- Printing the left boundary.
- Start from root.
- Iterate towards left node if it’s available else towards right node if it’s available. Keep on printing the node while traversing.
- Printing all leaves
- Start from root.
- Print all the leaves from the left subtree.
- Print all the leaves from the right subtree.
- Printing the right boundary.
- Start from root.
- Iterate towards right node if it’s available else towards left node if it’s available till we reach the leaf node.
- Keep on printing the node in reverse order while returning from recursive function.
Let’s have a look into sample function for boundary traversal.
void print_path_to_left_most_node (BinaryTree* root)
{
/* if leaf node thne it will be printed in 2nd step, ignore here */
if (!root->m_left && !root->m_right)
return;
cout << root->m_data << " ";
if (root->m_left)
print_path_to_left_most_node (root->m_left);
else if (root->m_right)
print_path_to_left_most_node (root->m_right);
}
void print_all_leaf_node (BinaryTree* root)
{
if (!root)
return;
print_all_leaf_node (root->m_left);
if (!root->m_left && !root->m_right) {
cout << root->m_data << " ";
return;
}
print_all_leaf_node (root->m_right);
}
void print_path_from_right_most_node (BinaryTree* root)
{
/* if leaf node thne it will be printed in 2nd step, ignore here */
if (!root->m_left && !root->m_right)
return;
if (root->m_right)
print_path_from_right_most_node (root->m_right);
else if (root->m_left)
print_path_from_right_most_node (root->m_left);
cout << root->m_data << " ";
}
void boundary_traversal (BinaryTree* root)
{
if (!root)
return;
/* Print path from root to left most node
Print all leaf node
Print path from right most node to root */
print_path_to_left_most_node (root);
print_all_leaf_node (root);
print_path_from_right_most_node (root->m_right);
}
Few of the functions used below are explained in Binary Tree implementation. Refer those before going ahead. Let’s define a main function to use above functions.
int main ()
{
BinaryTree* node1 = new BinaryTree (1);
BinaryTree* node2 = new BinaryTree (2);
BinaryTree* node3 = new BinaryTree (3);
BinaryTree* node4 = new BinaryTree (4);
BinaryTree* node5 = new BinaryTree (5);
BinaryTree* node6 = new BinaryTree (6);
BinaryTree* node7 = new BinaryTree (7);
BinaryTree* node8 = new BinaryTree (8);
BinaryTree* node9 = new BinaryTree (9);
BinaryTree* node10 = new BinaryTree (10);
/* Set node5 as root node */
/*
5
3 7
2 4 6 9
1 8 10
*/
BinaryTree* root = node5;
node5 -> m_left = node3;
node3 -> m_left = node2;
node3 -> m_right = node4;
node2 -> m_left = node1;
node5 -> m_right = node7;
node7 -> m_left = node6;
node7 -> m_right = node9;
node9 -> m_right = node10;
node9 -> m_left = node8;
print_tree (root);
cout << " Postorder Traversal: ";
postorder_traversal (root);
cout << endl;
boundary_traversal (root);
}
Let’s look into the output of above main function.
Binary tree contents: 5 3 2 1 4 7 6 9 8 10
Postorder Traversal: 1 2 4 3 6 8 10 9 7 5
5 3 2 1 4 6 8 10 9 7