A tree is a data structure similar to Linked list in which each node points to multiple nodes instead of simply pointing to the next node. A tree is called Binary tree if each node in a tree has maximum of two nodes.
An empty tree is also a Binary tree. We can call the two children of each node as Left and Right child of a node. The node of the tree which has no parent is called the Root of the tree. Perhaps Binary tree is the most used tree data structure in the programming world. Before going ahead have a look into Binary Tree basics and Binary Tree implementation.
Binary Tree Traversal
Binary Tree has multiple ways in which nodes can be accessed which is quite different that other data structures such as Stacks, Queues etc which follows one certain method such as LIFO, FIFO etc for accessing it’s elements.
There are multiple ways to traverse a Binary Tree.
- Inorder Traversal — In Inorder Traversal root node is visited in between it’s left and right child.
- Preorder Traversal — In Preorder Traversal root node is visited before it’s left and right child.
- Postorder Traversal — In Postorder Traversal root node is visited after it’s left and right child.
- Level order Traversal — In Level order Traversal, all the nodes present in same level is visited first and then their children will be visited.
In this article, we are going to talk about the LevelOrder Traversal.
Level Order Traversal
In Level order Traversal, all the nodes present in same level is visited first and then their children will be visited. Algorithm for Level Order traversal can be defined as mentioned below.
Algorithm
- Visit the root.
- While visiting nodes at level “l”, put all their children in a Queue.
- Dequeue from the Queue and visit all nodes.
- Repeat above two steps until all levels are visited in Binary Tree.
Let’s look into an example to understand it better.
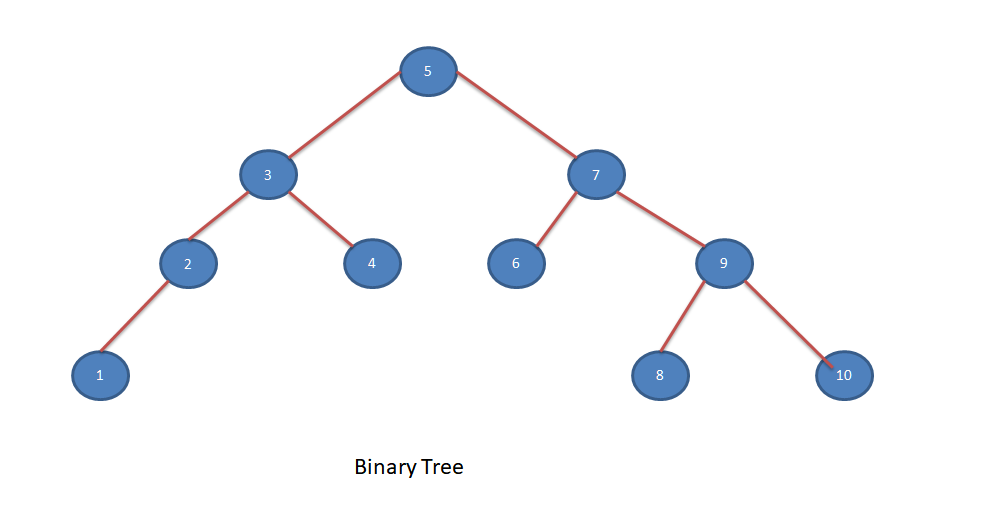
For the Binary tree mentioned in above image, Level Order traversal would be 5, 3, 7, 2, 4, 6, 9, 1, 8, 10
Important points
- In Level Order traversal first entry is always the root node present in the the tree.
- In Level Order traversal last entry is always the rightmost node present in the the tree.
- Looking into Level Order traversal, leftmost node can’t be identified.
Let’s have a look on basic class definition for Binary Tree.
class BinaryTree
{
public:
int m_data;
BinaryTree* m_left;
BinaryTree* m_right;
BinaryTree (int data);
BinaryTree (int data, BinaryTree* left, BinaryTree* right);
~BinaryTree ();
};
void print_binary_tree (BinaryTree* root)
{
cout << " " << root -> m_data;
if (root -> m_left)
print_binary_tree (root -> m_left);
if (root -> m_right)
print_binary_tree (root -> m_right);
}
void print_tree (BinaryTree* root)
{
cout << "Binary tree contents: ";
print_binary_tree (root);
cout << endl;
}
Few of the functions used below are explained in Generic Queue implementation. Refer those before going ahead.
Let’s look into the sample code for Level Order Traversal.
/* Class definition for Queue used in Level Order traversal */
class Queue
{
private:
int m_front;
int m_rear;
int m_entries;
int m_max_size;
BinaryTree** m_queue;
public:
Queue (int max);
~Queue ();
int size ();
int maxSize ();
BinaryTree* enqueue (BinaryTree* entry);
BinaryTree* dequeue ();
bool isEmpty ();
BinaryTree* atFront ();
void print_content ()
{
int temp = m_rear;
while (temp != m_front)
{
cout << (m_queue[temp]) -> m_data << " ";
temp = (temp + 1) % m_max_size;
}
cout << endl;
}
};
void levelorder_traversal (BinaryTree* root)
{
if (!root)
return;
Queue q(20);
BinaryTree* temp = root;
while (temp)
{
cout << " " << temp -> m_data;
if (temp -> m_left)
q.enqueue (temp -> m_left);
if (temp -> m_right)
q.enqueue (temp -> m_right);
if (!q.isEmpty ())
temp = q.dequeue ();
else
temp = NULL;
}
}
Few of the functions used below are explained in Binary Tree Implementation. Refer those before going ahead.
Let’s define a main function to use above functions.
int main ()
{
BinaryTree* node1 = new BinaryTree (1);
BinaryTree* node2 = new BinaryTree (2);
BinaryTree* node3 = new BinaryTree (3);
BinaryTree* node4 = new BinaryTree (4);
BinaryTree* node5 = new BinaryTree (5);
BinaryTree* node6 = new BinaryTree (6);
BinaryTree* node7 = new BinaryTree (7);
BinaryTree* node8 = new BinaryTree (8);
BinaryTree* node9 = new BinaryTree (9);
BinaryTree* node10 = new BinaryTree (10);
/* Set node5 as root node */
BinaryTree* root = node5;
node5 -> m_left = node3;
node3 -> m_left = node2;
node3 -> m_right = node4;
node2 -> m_left = node1;
node5 -> m_right = node7;
node7 -> m_left = node6;
node7 -> m_right = node9;
node9 -> m_right = node10;
node9 -> m_left = node8;
print_tree (root);
cout << " LevelOrder Traversal: ";
levelorder_traversal (root);
cout << endl;
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 5 3 2 1 4 7 6 9 8 10
LevelOrder Traversal: 5 3 7 2 4 6 9 1 8 10
Level Order Traversal Applications
Level Order traversal mainly used as a Breadth First Search (BFS).