A tree is a data structure similar to Linked list in which each node points to multiple nodes instead of simply pointing to the next node. A tree is called Binary tree if each node in a tree has maximum of two nodes.
An empty tree is also a Binary tree. We can call the two children of each node as Left and Right child of a node. The node of the tree which has no parent is called the Root of the tree. Perhaps Binary tree is the most used tree data structure in the programming world.
Examples of Binary tree
Below are some examples of binary tree.
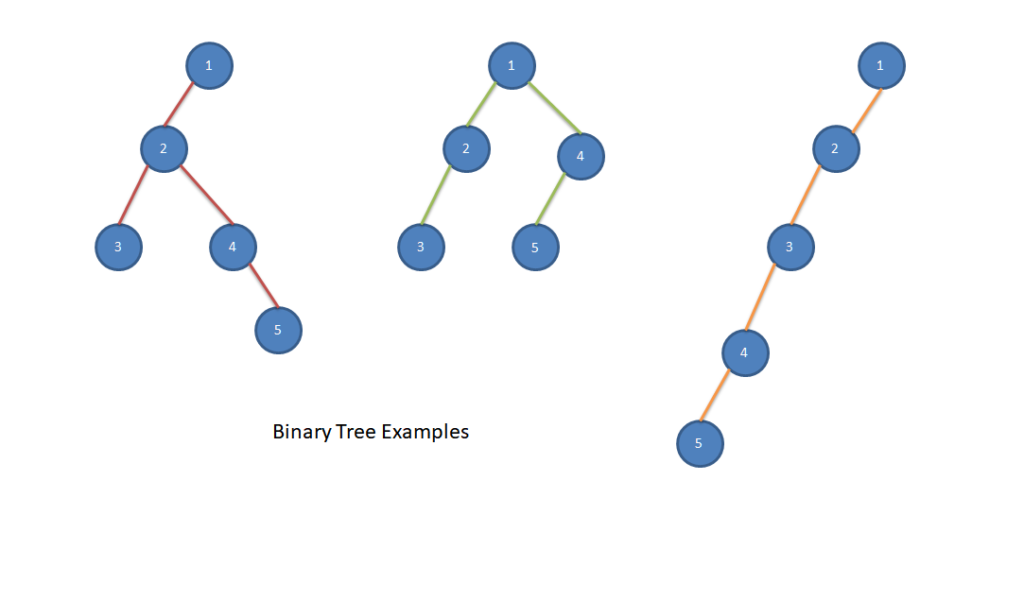
Types of Binary Tree
Binary tree can be broadly classified into three categories
Strict Binary tree

If in a binary tree, each node has either exactly two children or no children then this binary tree is called as Strict Binary tree.
Full Binary Tree
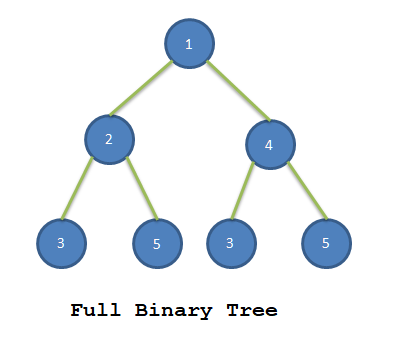
If in a binary tree, each node has exactly two children and all the leaf nodes are the same level of the tree then this binary tree is called as Full Binary tree.
Complete Binary Tree
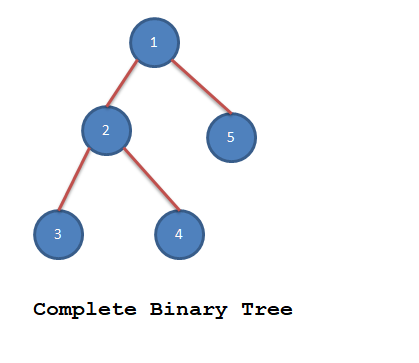
If in a binary tree all leaf nodes are present at height “h” or “h – 1” then this binary tree is called Complete Binary tree.
Properties of Binary Tree
| Property | Value |
|---|---|
| Number of nodes at level “h” | 2h |
| Total number of nodes (tree with level “h”) | 2h+1 – 1 |
| Complete binary tree nodes count | Minimum Nodes: 2h Maximum node: 2h+1 – 1 |
| Number of leaf nodes in full binary tree | 2h |
| Number of NULL pointers in complete binary tree (with “n” Nodes) | n + 1 |
| Minimum number of levels possible in a binary tree | log2(n+1) – 1 (root is at level 0) |
Binary tree applications
- Expression tree in compilers
- Huffman coding algorithm
- Binary search tree
- Priority Queues