A tree is a data structure similar to Linked list in which each node points to multiple nodes instead of simply pointing to the next node. A tree is called Binary tree if each node in a tree has maximum of two nodes.
An empty tree is also a Binary tree. We can call the two children of each node as Left and Right child of a node. The node of the tree which has no parent is called the Root of the tree. Perhaps Binary tree is the most used tree data structure in the programming world. Before going ahead have a look into Binary Tree basics and Binary Tree Implementation.
Deleting an element in Binary Tree
Deleting a node in Binary tree is a big task as it involves following sub tasks.
- Search node and it’s parent node in the Binary Tree
- Rebalance the binary tree, adjust children of the deleted node
Let’s look into an example to understand the procedure before looking into the sample code.
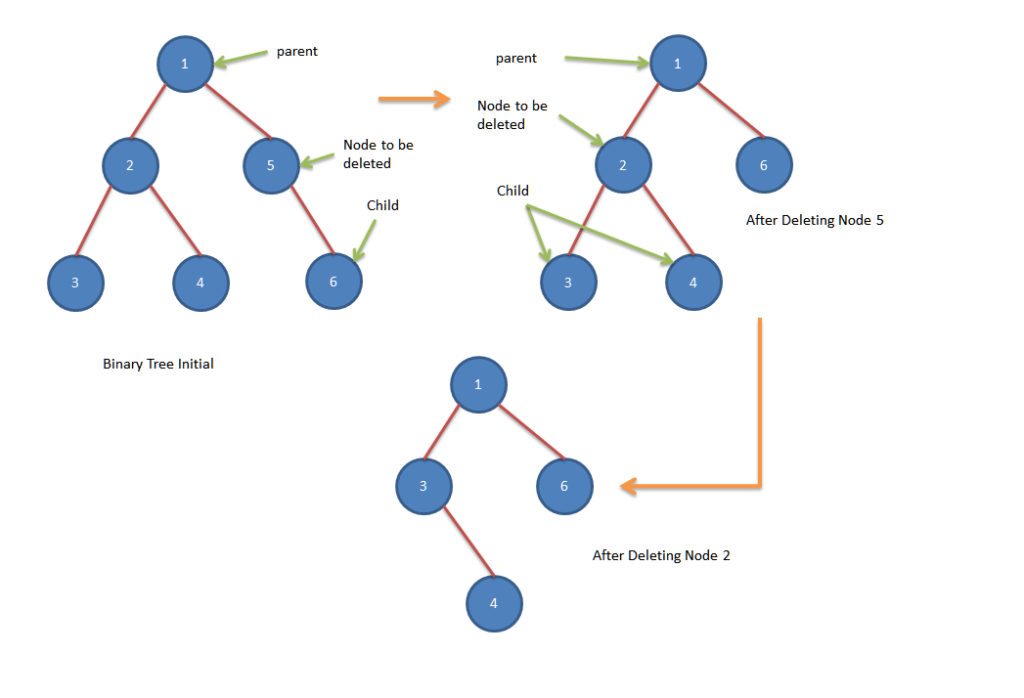
Search node and it’s parent node in the Binary Tree
For deleting a node in Binary tree, we need to find the parent node of the node to be deleted as parent node pointers need to be adjusted.
Let’s look into the sample code for finding the parent of a node in Binary Tree.
BinaryTree* find_parent_node (BinaryTree* root, int searchData)
{
if (!root)
{
return NULL;
}
if ((root -> m_left && root -> m_left -> m_data == searchData) || (root -> m_right && root -> m_right -> m_data == searchData))
{
return root;
}
BinaryTree* temp = find_parent_node (root -> m_left, searchData);
if (!temp)
{
return find_parent_node (root -> m_right, searchData);
}
return temp;
}
Rebalance the binary tree, adjust children of the deleted node
In order to delete a node, we need to adjust the child nodes of the deleted node and put them into new places as a child of some other node. This step is very important otherwise few nodes will be lost after this operation.
Once both children of the node to be deleted is adjusted to their new places then nodes can be deleted.
Let’s look into the sample code.
void delete_node_and_rebalance (BinaryTree** root, BinaryTree* parent, int searchData)
{
if (!parent)
{
/* Root node needs to be deleted */
BinaryTree* newRoot = NULL;
if (root)
{
if ((*root) -> m_left)
{
newRoot = (*root) -> m_left;
if ((*root) -> m_right)
{
insert_at_first_available_place (newRoot, (*root) -> m_right);
}
}
else
{
newRoot = (*root) -> m_left;
}
delete (*root);
*root = newRoot;
return;
}
cout << "Root and Parent both not set !!!" << endl;
return;
}
if (parent -> right && parent -> m_right -> m_data == searchData)
{
BinaryTree* temp = parent -> m_right;
parent -> m_right = NULL;
insert_at_first_available_place (*root, temp -> m_left);
insert_at_first_available_place (*root, temp -> m_right);
delete temp;
}
else
{
/* We don't need to check for left pointer validity as we know this node
is a parent node and since right child is not matching the searched data,
Hence left node will surely match the data */
BinaryTree* temp = parent -> m_left;
parent -> m_left = NULL;
insert_at_first_available_place (*root, temp -> m_left);
insert_at_first_available_place (*root, temp -> m_right);
delete temp;
}
return;
}
We can define a wrapper function for the deletion of a node which will act as an interface function for deleting a node in Binary Tree and can be called from outside directly.
Let’s look into the sample code.
BinaryTree* delete_node (BinaryTree* root, int searchData)
{
if (!root)
{
cout << "Empty Binary Tree, Nothing to Delete !!!" << endl;
}
if (root -> m_data == searchData)
{
delete_node_and_rebalance (&root, NULL, searchData);
return root;
}
BinaryTree* parent_node = find_parent_node (root, searchData);
if (!parent_node)
{
cout << "Searched node: " << searchData << " not found, Nothing to Delete !!!" << endl;
}
else
{
delete_node_and_rebalance (&root, parent_node, searchData);
}
return root;
}
Deleting all nodes in Binary Tree
As we saw earlier, each node memory is dynamically allocated in Binary Tree hence all the memory should be freed accordingly once the usage of Binary tree is done. Since we need to delete all nodes of the Binary Tree, Hence we don’t need to rebalance the children of the node to be deleted as all of them are about to be deleted.
Let’s look into the sample code for deleting all nodes in Binary Tree.
void delete_all_nodes (BinaryTree* root)
{
if (!root)
return;
if (root -> m_left)
{
delete_all_nodes (root -> m_left);
}
if (root -> m_right)
{
delete_all_nodes (root -> m_right);
}
delete root;
}
Few of the functions used below are explained in Binary Tree Implementation. Refer those before going ahead.
Let’s look into the sample main function which utilizes Binary Tree class definition and functions defined above.
void print_tree (BinaryTree* root)
{
cout << "Binary tree contents: ";
print_binary_tree (root);
cout << endl;
}
int main ()
{
BinaryTree* root = new BinaryTree(20);
insert_after_certain_element (root, 10, 20);
insert_after_certain_element (root, 30, 20);
insert_after_certain_element (root, 40, 20);
insert_after_certain_element (root, 1, 40);
insert_after_certain_element (root, 50, 30);
insert_after_certain_element (root, 60, 20);
print_tree (root);
root = delete_node (root, 20);
print_tree (root);
root = delete_node (root, 40);
print_tree (root);
root = delete_node (root, 100);
if (search_node_in_binary_tree (root, 1))
{
cout << "Searched data: 1 found in binary tree" << endl;
}
else
{
cout << "Searched data: 1 not found" << endl;
}
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 20 10 40 1 60 30 50
Binary tree contents: 10 40 1 30 50 60
Binary tree contents: 10 1 30 50 60
Searched node: 100 not found, Nothing to Delete !!!
Searched data: 1 found in binary tree