A Binary Search Tree is a Binary tree in which all the nodes has following properties.
- Left subtree of a node contains all the nodes having values lesser than the node.
- Right subtree of a node contains all the nodes having values higher than the node.
- Both the left and right subtree is also a Binary Search Tree.
As the name suggests, this data structure is mainly used for faster searching. In order to do that, restrictions are applied while inserting/deleting an element into the tree. As a result of these restrictions, worst case search time complexity remains at O(log n). Before going ahead have a look into Binary Search Tree basics.
Binary Search Tree Implementation
Here we are going to talk about a very simple implementation of Binary Search tree using Linked List similar data structure. Also we will discuss about Deletion operation in Binary Search Tree.
Before looking into Insertion operation detail let’s look into basic C++ class definition for Binary Search Tree.
template <typename T>
class BinarySearchTree
{
public:
T m_data;
BinarySearchTree* m_left;
BinarySearchTree* m_right;
BinarySearchTree (T data);
~BinarySearchTree ();
};
Binary Search Tree Class Function Implementation
Let’s have a look into all the functions/operations definition of Binary Search Tree Class.
Constructor/Destructor implementation
/* This constructor will be called when an isolated node is created */
template <typename T>
BinarySearchTree<T>::BinarySearchTree(T data): m_data(data),
m_left (NULL),
m_right (NULL)
{}
/* No dynamic allocation is being done, hence nothing to delete here */
template <typename T>
BinarySearchTree<T>::~BinarySearchTree ()
{}
Searching an element
This is the main operation of Binary Search Tree. Since a node value is higher than it’s left subtree and lower than it’s right subtree, hence in every comparison searching moves into either left subtree or towards right subtree. So, after every comparison basically one side of the tree is completely skipped, thus resulting into a faster search.
Algorithm
- Start from the root. If root is empty is then node is not present.
- If searched data is higher than root node value then go towards right child of the root else traverse towards left child.
- If there is no child present then searched element is not present in Binary Search Tree else repeat step 2 and step 3.
Let’s take an example of Binary Search Tree to understand how searching of an element works.
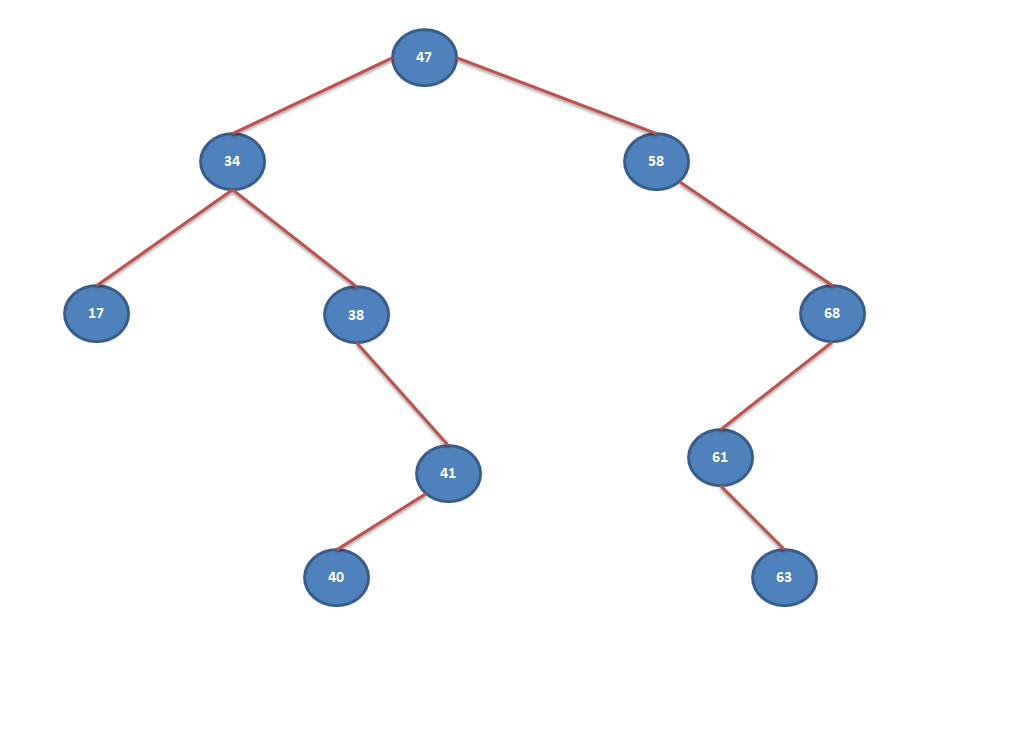
Here we are going to explain how search works with an example. Let’s assume we need to search element “61” in the above BST.
- Start with Root, Searched data “61” is higher than root node “47”. Hence traverse towards right child.
- Searched data “61” is higher than next node “58”. Hence move towards right.
- Searched data “61” is lower than next node “68”. Hence move towards left.
- Searched data “61” is same as next node and we found the searched node.
This operation can be implemented in both iterative and recursive manner.
Searching an element using iterations
Let’s look into the sample code.
template <typename T>
void search_element_in_bst (T data, BinarySearchTree<T>* root)
{
BinarySearchTree<T>* temp = root;
while (temp)
{
if (temp -> m_data == data)
{
cout << "Data: " << data << " found in BST !!!" << endl;
return;
}
else if (temp -> m_data > data)
{
temp = temp -> m_left;
}
else
{
temp = temp -> m_right;
}
}
cout << "Data: " << data << " not found in BST !!!" << endl;
}
Searching an element using recursion
Let’s look into the sample code.
template <typename T>
void search_element_in_bst_recursive (T data, BinarySearchTree<T>* root)
{
BinarySearchTree<T>* temp = root;
if (!temp)
{
cout << "Data: " << data << " not found in BST !!!" << endl;
return;
}
if (temp -> m_data == data)
{
cout << "Data: " << data << " found in BST !!!" << endl;
return;
}
else if (temp -> m_data > data)
{
search_element_in_bst_recursive (data, temp -> m_left);
}
else
{
search_element_in_bst_recursive (data, temp -> m_right);
}
}
Few of the functions defined below are explained in Binary Search Tree Insert Operation Explanation and Binary Search Tree Delete Operation Explanation.
Let’s look into the sample main function which utilizes Binary Search Tree class definition and iterative functions defined above.
template <typename T>
void print_binary_tree_inorder (BinarySearchTree<T>* root)
{
if (root -> m_left)
print_binary_tree_inorder (root -> m_left);
cout << " " << root -> m_data;
if (root -> m_right)
print_binary_tree_inorder (root -> m_right);
}
template <typename T>
void print_tree (BinarySearchTree<T>* root)
{
cout << "Binary tree contents: ";
print_binary_tree_inorder (root);
cout << endl;
}
/* Simply used this function to delete all nodes and free memory */
template <typename T>
void delete_all_nodes (BinarySearchTree<T>* root)
{
if (!root)
return;
if (root -> m_left)
{
delete_all_nodes (root -> m_left);
}
if (root -> m_right)
{
delete_all_nodes (root -> m_right);
}
delete root;
}
int main ()
{
BinarySearchTree<int>* root = new BinarySearchTree<int> (33);
insert_element_in_bst (20, root);
insert_element_in_bst (10, root);
insert_element_in_bst (30, root);
insert_element_in_bst (40, root);
insert_element_in_bst (50, root);
insert_element_in_bst (43, root);
insert_element_in_bst (77, root);
insert_element_in_bst (69, root);
insert_element_in_bst (25, root);
insert_element_in_bst (11, root);
insert_element_in_bst (10, root);
insert_element_in_bst (5, root);
insert_element_in_bst (18, root);
insert_element_in_bst (67, root);
insert_element_in_bst (88, root);
insert_element_in_bst (99, root);
insert_element_in_bst (65, root);
insert_element_in_bst (58, root);
insert_element_in_bst (51, root);
insert_element_in_bst (77, root);
print_tree (root);
search_element_in_bst (57, root);
search_element_in_bst (20, root);
search_element_in_bst (50, root);
root = delete_element_in_bst (20, root);
print_tree (root);
root = delete_element_in_bst (33, root);
print_tree (root);
root = delete_element_in_bst (10, root);
print_tree (root);
root = delete_element_in_bst (77, root);
print_tree (root);
root = delete_element_in_bst (135, root);
print_tree (root);
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 5 10 10 11 18 20 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 57 not found in BST !!!
Data: 20 found in BST !!!
Data: 50 found in BST !!!
Data: 20 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 33 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 10 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 77 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Data: 135 not found in BST !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Few of the functions defined below are explained in Binary Search Tree Insert Operation Explanation and Binary Search Tree Delete Operation Explanation.
Let’s look into the sample main function which utilizes Binary Search Tree class definition and recursive functions defined above.
int main ()
{
BinarySearchTree<int>* root = new BinarySearchTree<int> (33);
insert_element_in_bst_recursive (20, root);
insert_element_in_bst_recursive (10, root);
insert_element_in_bst_recursive (30, root);
insert_element_in_bst_recursive (40, root);
insert_element_in_bst_recursive (50, root);
insert_element_in_bst_recursive (43, root);
insert_element_in_bst_recursive (77, root);
insert_element_in_bst_recursive (69, root);
insert_element_in_bst_recursive (25, root);
insert_element_in_bst_recursive (11, root);
insert_element_in_bst_recursive (10, root);
insert_element_in_bst_recursive (5, root);
insert_element_in_bst_recursive (18, root);
insert_element_in_bst_recursive (67, root);
insert_element_in_bst_recursive (88, root);
insert_element_in_bst_recursive (99, root);
insert_element_in_bst_recursive (65, root);
insert_element_in_bst_recursive (58, root);
insert_element_in_bst_recursive (51, root);
insert_element_in_bst_recursive (77, root);
print_tree (root);
search_element_in_bst_recursive (57, root);
search_element_in_bst_recursive (20, root);
search_element_in_bst_recursive (50, root);
BinarySearchTree<int>* parent = NULL;
root = delete_element_in_bst_recursive (20, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (33, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (10, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (77, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (135, root, parent);
print_tree (root);
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 5 10 10 11 18 20 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 57 not found in BST !!!
Data: 20 found in BST !!!
Data: 50 found in BST !!!
Data: 20 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 33 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 10 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 77 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Data: 135 not found in BST !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99