A Binary Search Tree is a Binary tree in which all the nodes has following properties.
- Left subtree of a node contains all the nodes having values lesser than the node.
- Right subtree of a node contains all the nodes having values higher than the node.
- Both the left and right subtree is also a Binary Search Tree.
As the name suggests, this data structure is mainly used for faster searching. In order to do that, restrictions are applied while inserting/deleting an element into the tree. As a result of these restrictions, worst case search time complexity remains at O(log n).
Examples of Binary Search Tree
Below are some examples of Binary Search Trees.
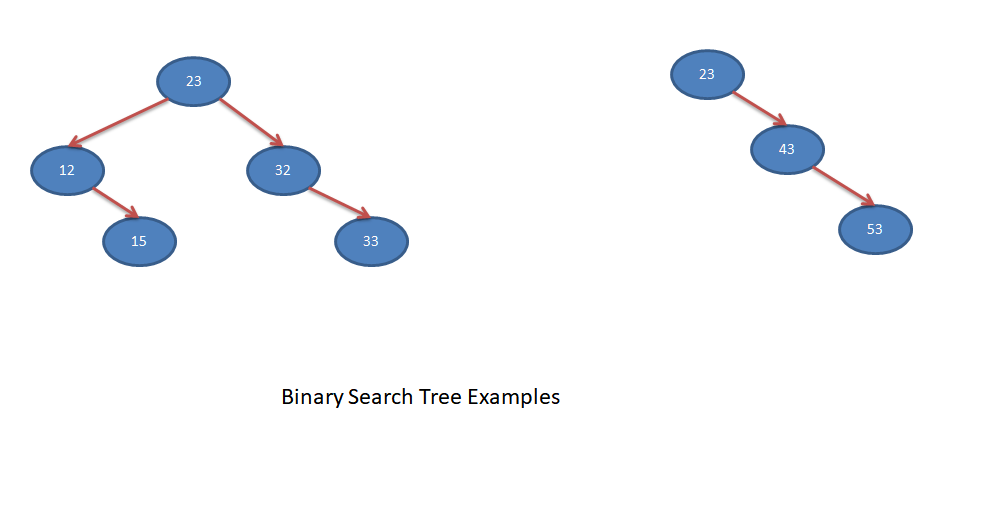
Binary Search Tree Operations
Inserting an element
In order to insert an element in a Binary Search Tree, first we need to find a place for this new element and then we need to add the element at that specific place. Note that, after inserting any element in Binary Search Tree, it’s property must be retained.
Deleting an element
In order to delete an element in a Binary Search Tree, first we need to search for the element and then we need to delete the element. Note that, after deleting any element in Binary Search Tree, it’s property must be retained.
Searching an element
This is the main operation of Binary Search Tree. Since a node value is higher than it’s left subtree and lower than it’s right subtree, hence in every comparison searching moves into either left subtree or towards right subtree. So, after every comparison basically one side of the tree is completely skipped, thus resulting into a faster search.
Properties of Binary Search Tree
Since a node value is higher than it’s left subtree and lower than it’s right subtree, hence an inorder traversal will produce a sorted list of elements.
Applications of Binary Search Tree
- Used for indexing
- Used in search algorithms
- helpful in maintaining a sorted stream of data
- Can be used as Priority Queues