A Binary Search Tree is a Binary tree in which all the nodes has following properties.
- Left subtree of a node contains all the nodes having values lesser than the node.
- Right subtree of a node contains all the nodes having values higher than the node.
- Both the left and right subtree is also a Binary Search Tree.
As the name suggests, this data structure is mainly used for faster searching. In order to do that, restrictions are applied while inserting/deleting an element into the tree. As a result of these restrictions, worst case search time complexity remains at O(log n). Before going ahead have a look into Binary Search Tree basics.
Binary Search Tree Implementation
Here we are going to talk about a very simple implementation of Binary Search tree using Linked List similar data structure. Also we will discuss about Deletion operation in Binary Search Tree.
Before looking into Insertion operation detail let’s look into basic C++ class definition for Binary Search Tree.
template <typename T>
class BinarySearchTree
{
public:
T m_data;
BinarySearchTree* m_left;
BinarySearchTree* m_right;
BinarySearchTree (T data);
~BinarySearchTree ();
};
Binary Search Tree Class Function Implementation
Let’s have a look into all the functions/operations definition of Binary Search Tree Class.
Constructor/Destructor implementation
/* This constructor will be called when an isolated node is created */
template <typename T>
BinarySearchTree<T>::BinarySearchTree(T data): m_data(data),
m_left (NULL),
m_right (NULL)
{}
/* No dynamic allocation is being done, hence nothing to delete here */
template <typename T>
BinarySearchTree<T>::~BinarySearchTree ()
{}
Deleting an element
In order to delete an element in a Binary Search Tree, first we need to search for the element and then we need to delete the element.
Note that, after deleting any element in Binary Search Tree, it’s property must be retained.
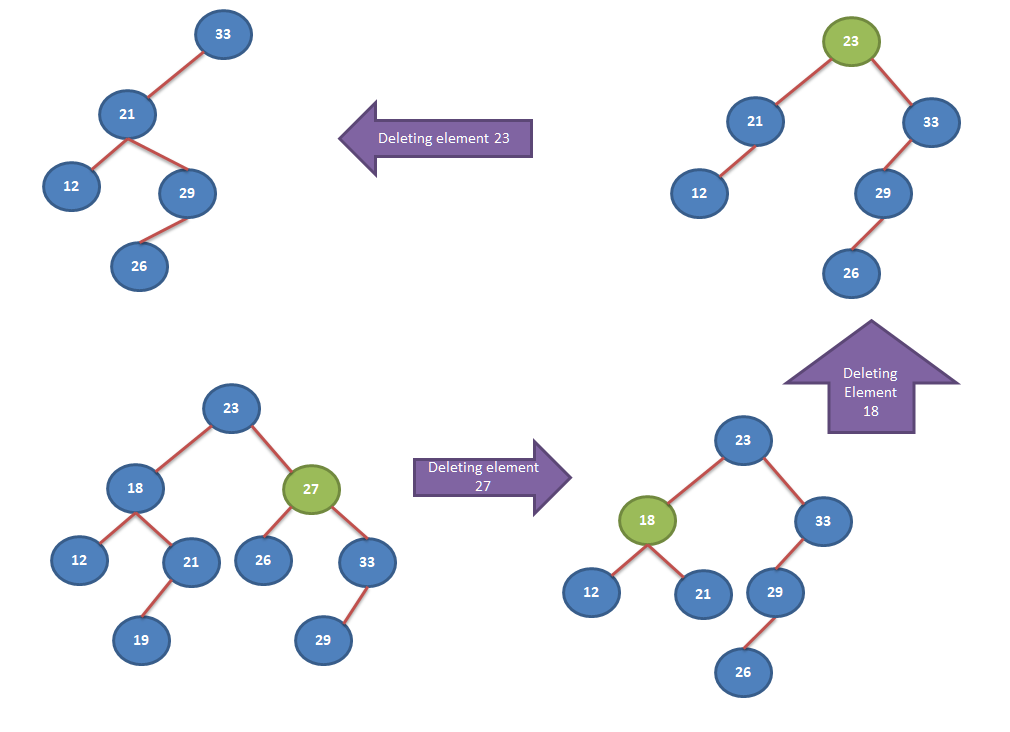
As shown in above diagram, after deletion of a mentioned node, Binary Search Tree properties are still holding correctly. In this article we will look into methods for inserting an element into Binary Search Tree.
Algorithm
- Search the node which needs to be deleted.
- if node doesn’t have any child then set the parent’s pointer to NULL and delete the node.
- If node has one child then set the parent’s pointer to the child and delete the node.
- If node has two child then
- set the parent’s pointer to right child of the node.
- insert the node’s left child as the child of node’s right child to it’s appropriate place (check BST insertion for more information).
Deletion operation can be implemented in both iterative and recursive manner.
Deleting an element using iterations
Let’s look into the sample code.
template <typename T>
BinarySearchTree<T>* delete_element_in_bst (T data, BinarySearchTree<T>* root)
{
BinarySearchTree<T>* temp = root;
BinarySearchTree<T>* parent = NULL;
while (temp)
{
if (temp -> m_data == data)
{
cout << "Data: " << data << " found in BST, node will be deleted now !!!" << endl;
BinarySearchTree<T>* left_child = temp -> m_left;
BinarySearchTree<T>* new_root = root;
if (parent)
{
if (parent -> m_left == temp)
{
parent -> m_left = temp -> m_right;
insert_node_in_bst (left_child, parent -> m_left);
}
else
{
parent -> m_right = temp -> m_right;
insert_node_in_bst (left_child, parent -> m_right);
}
}
else
{
/* Deleted node is root node */
new_root = temp -> m_right;
insert_node_in_bst (temp -> m_left, new_root);
}
delete temp;
return new_root;
}
else
{
parent = temp;
if (temp -> m_data > data)
{
temp = temp -> m_left;
}
else
{
temp = temp -> m_right;
}
}
}
cout << "Data: " << data << " not found in BST !!!" << endl;
return root;
}
Deleting an element using recursion
Let’s look into the sample code.
template <typename T>
BinarySearchTree<T>* delete_element_in_bst_recursive (T data, BinarySearchTree<T>* root, BinarySearchTree<T>* parent)
{
BinarySearchTree<T>* temp = root;
BinarySearchTree<T>* new_root = NULL;
if (!temp)
{
cout << "Data: " << data << " not found in BST !!!" << endl;
return parent;
}
if (temp -> m_data == data)
{
cout << "Data: " << data << " found in BST, node will be deleted now !!!" << endl;
BinarySearchTree<T>* left_child = temp -> m_left;
if (parent)
{
if (parent -> m_left == temp)
{
parent -> m_left = temp -> m_right;
insert_node_in_bst (left_child, parent -> m_left);
}
else
{
parent -> m_right = temp -> m_right;
insert_node_in_bst (left_child, parent -> m_right);
}
}
else
{
/* Deleted node is root node */
new_root = temp -> m_right;
insert_node_in_bst (temp -> m_left, new_root);
}
delete temp;
return new_root;
}
else
{
if (temp -> m_data > data)
{
new_root = delete_element_in_bst_recursive (data, temp -> m_left, temp);
}
else
{
new_root = delete_element_in_bst_recursive (data, temp -> m_right, temp);
}
}
return root;
}
Few of the functions defined below are explained in Binary Search Tree Insert Operation Explanation.
Let’s look into the sample main function which utilizes Binary Search Tree class definition and iterative functions defined above.
template <typename T>
void print_binary_tree_inorder (BinarySearchTree<T>* root)
{
if (root -> m_left)
print_binary_tree_inorder (root -> m_left);
cout << " " << root -> m_data;
if (root -> m_right)
print_binary_tree_inorder (root -> m_right);
}
template <typename T>
void print_tree (BinarySearchTree<T>* root)
{
cout << "Binary tree contents: ";
print_binary_tree_inorder (root);
cout << endl;
}
/* Simply used this function to delete all nodes and free memory */
template <typename T>
void delete_all_nodes (BinarySearchTree<T>* root)
{
if (!root)
return;
if (root -> m_left)
{
delete_all_nodes (root -> m_left);
}
if (root -> m_right)
{
delete_all_nodes (root -> m_right);
}
delete root;
}
int main ()
{
BinarySearchTree<int>* root = new BinarySearchTree<int> (33);
insert_element_in_bst (20, root);
insert_element_in_bst (10, root);
insert_element_in_bst (30, root);
insert_element_in_bst (40, root);
insert_element_in_bst (50, root);
insert_element_in_bst (43, root);
insert_element_in_bst (77, root);
insert_element_in_bst (69, root);
insert_element_in_bst (25, root);
insert_element_in_bst (11, root);
insert_element_in_bst (10, root);
insert_element_in_bst (5, root);
insert_element_in_bst (18, root);
insert_element_in_bst (67, root);
insert_element_in_bst (88, root);
insert_element_in_bst (99, root);
insert_element_in_bst (65, root);
insert_element_in_bst (58, root);
insert_element_in_bst (51, root);
insert_element_in_bst (77, root);
print_tree (root);
root = delete_element_in_bst (20, root);
print_tree (root);
root = delete_element_in_bst (33, root);
print_tree (root);
root = delete_element_in_bst (10, root);
print_tree (root);
root = delete_element_in_bst (77, root);
print_tree (root);
root = delete_element_in_bst (135, root);
print_tree (root);
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 5 10 10 11 18 20 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 20 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 33 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 10 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 77 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Data: 135 not found in BST !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Few of the functions defined below are explained in Binary Search Tree Insert Operation Explanation.
Let’s look into the sample main function which utilizes Binary Search Tree class definition and recursive functions defined above.
int main ()
{
BinarySearchTree<int>* root = new BinarySearchTree<int> (33);
insert_element_in_bst_recursive (20, root);
insert_element_in_bst_recursive (10, root);
insert_element_in_bst_recursive (30, root);
insert_element_in_bst_recursive (40, root);
insert_element_in_bst_recursive (50, root);
insert_element_in_bst_recursive (43, root);
insert_element_in_bst_recursive (77, root);
insert_element_in_bst_recursive (69, root);
insert_element_in_bst_recursive (25, root);
insert_element_in_bst_recursive (11, root);
insert_element_in_bst_recursive (10, root);
insert_element_in_bst_recursive (5, root);
insert_element_in_bst_recursive (18, root);
insert_element_in_bst_recursive (67, root);
insert_element_in_bst_recursive (88, root);
insert_element_in_bst_recursive (99, root);
insert_element_in_bst_recursive (65, root);
insert_element_in_bst_recursive (58, root);
insert_element_in_bst_recursive (51, root);
insert_element_in_bst_recursive (77, root);
print_tree (root);
BinarySearchTree<int>* parent = NULL;
root = delete_element_in_bst_recursive (20, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (33, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (10, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (77, root, parent);
print_tree (root);
root = delete_element_in_bst_recursive (135, root, parent);
print_tree (root);
delete_all_nodes (root);
}
Let’s analyze the output of this main function.
Binary tree contents: 5 10 10 11 18 20 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 20 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 33 40 43 50 51 58 65 67 69 77 77 88 99
Data: 33 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 10 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 77 88 99
Data: 77 found in BST, node will be deleted now !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99
Data: 135 not found in BST !!!
Binary tree contents: 5 10 11 18 25 30 40 43 50 51 58 65 67 69 77 88 99