AVL Tree Self Balancing Rotations – Left Rotation explained

An AVL (Adelson-Velskii and Landis) Tree is a self balancing Binary Search Tree which has the following properties.

For any node “A”, the height of the left subtree of “A” and height of the right subtree of “A” differ by 1 at max.

In case of Binary search Trees worst case search complexity is O(n) in cases when the Binary Search Tree is skewed. In AVL tree, since heights of left and right subtree are balanced, hence search complexity improves to O(log n). Before going ahead have a look into AVL Tree Basics.

AVL Tree Class definition

Since AVL Tree is a Binary Search Tree also, hence in all code below we have used the same property to show how to use inheritance effectively.
In below code, we have define AVL class as a derived class of Binary Search Tree Base class. Please check here for more information related to Binary Search Tree implementations before going ahead.
Let’s have a look into basic C++ class definition for AVL Tree.

template <typename T>
class BinarySearchTree
{
    public:
        T m_data;
        BinarySearchTree* m_left;
        BinarySearchTree* m_right;

        BinarySearchTree (T data);
        virtual ~BinarySearchTree ();
};

template <typename T>
class AVL: public BinarySearchTree<T>
{
    public:
        int m_height;
        AVL (T data);
        ~AVL ();
};

template <typename T>
AVL<T>::AVL (T data):BinarySearchTree<T> (data), m_height (0)
{}

template <typename T>
AVL<T>::~AVL ()
{}

AVL Tree Rotations

Whenever a new element is inserted into an AVL Tree, there is a chance of AVL tree becoming unbalanced. In order to rebalance AVL tree again to satisfy the height criteria, AVL tree rotations are performed.
In order to rebalance the tree, we start at the node inserted and travel up the tree, balancing each and every node of the tree if needed.

Left Rotations

In this rotation operation, right child “R” of the unbalanced node “A” replaced the unbalanced node position and unbalanced node “A” becomes the left child of the replacing node “R”. If node “R” has any existing left child
then it will be moved as the right child of unbalanced node “A”. Let’s look into below example to understand it better.

Let’s take an example to understand it better.

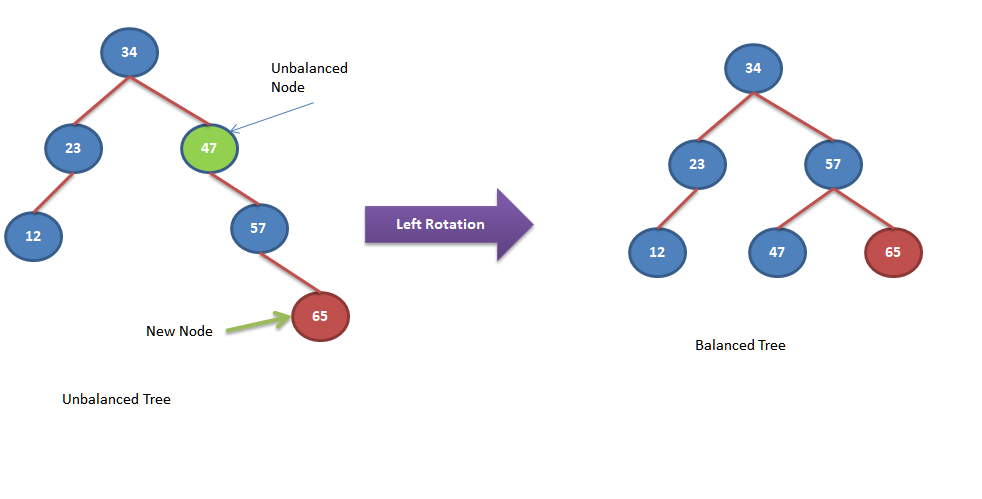
As you can see in the above example node “47” becomes unbalanced after insertion of new node “65”.

Condition for Left Rotations

Left rotation operation is being applied only when following condition is met.

• After insertion of new node,
  • if the parent node of the new node has higher right subtree than left subtree by >= 2
  • new node is added as the right child of the parent’s right child.

Algorithm

• Insert the new node at it’s location using Binary Search Tree insertion algorithm
• Check the height_balance of the parent node.
  • if the parent node of the new node has higher right subtree than left subtree by >= 2
  • new node is added as the right child of the parent’s right child.
• if above condition holds good then
  • parent’s right child becomes the new parent.
  • current parent becomes the left child of new parent.
  • if new parent has any left child then it becomes the right child of current parent.
• return the new parent node.

Let’s look into the sample code for this.

/* Left Rotate 
 *          x                      z
 *         / \                    / \
 *        y   z                  x   b
 *           / \     ---->      / \   \
 *          a   b              y   a   c
 *               \
 *  new entry --> c
*/
template <typename T>
AVL<T>* left_rotate (AVL<T>* node_to_be_balanced)
{
    AVL<T>* temp = dynamic_cast<AVL<T>*> (node_to_be_balanced -> m_right);
    AVL<T>* left_child = dynamic_cast<AVL<T>*> (node_to_be_balanced -> m_right -> m_left);
    temp -> m_left = node_to_be_balanced;
    node_to_be_balanced -> m_right = left_child;
    
    node_to_be_balanced -> m_height = height_of_node (node_to_be_balanced);
    temp -> m_height = height_of_node (temp);
    return temp;
}

Height of the node function definition

template <typename T>
int height_of_node (BinarySearchTree<T>* root)
{
    if (!root)
        return 0;

    int left = height_of_node (root -> m_left);
    int right = height_of_node (root -> m_right);

    if (left > right)
        return 1 + left;
    else
        return 1 + right;
}

For checking out the usage of this function, check AVL Tree Insertion and AVL Tree Deletion operation.