Binary Search Tree / Interview Questions / Programming Questions / Tree

AVL Tree Insertion Of Node Explained With Simple Example

adminby admin

An AVL (Adelson-Velskii and Landis) Tree is a self balancing Binary Search Tree which has the following properties.

For any node “A”, the height of the left subtree of “A” and height of the right subtree of “A” differ by 1 at max.

In case of Binary search Trees worst case search complexity is O(n) in cases when the Binary Search Tree is skewed. In AVL tree, since heights of left and right subtree are balanced, hence search complexity improves to O(log n). Before going ahead have a look into AVL Tree Basics.

AVL Tree Class definition

Since AVL Tree is a Binary Search Tree also, hence in all code below we have used the same property to show how to use inheritance effectively.
In below code, we have define AVL class as a derived class of Binary Search Tree Base class. Please check here for more information related to Binary Search Tree implementations before going ahead.
Let’s have a look into basic C++ class definition for AVL Tree.

template <typename T>
class BinarySearchTree
{
    public:
        T m_data;
        BinarySearchTree* m_left;
        BinarySearchTree* m_right;

        BinarySearchTree (T data);
        virtual ~BinarySearchTree ();
};

template <typename T>
class AVL: public BinarySearchTree<T>
{
    public:
        int m_height;
        AVL (T data);
        ~AVL ();
};

template <typename T>
AVL<T>::AVL (T data):BinarySearchTree<T> (data), m_height (0)
{}

template <typename T>
AVL<T>::~AVL ()
{}

Inserting an element

In order to insert an element in AVL tree, first we need to find the place in the existing AVL using Binary Search Tree Insertion Algorithm. After inserting the element to it’s correct place, all the nodes in the path from root to this new node will be checked for balanced condition required for AVL tree. If any node in AVL Tree is found to be unbalanced then using

methods AVL tree node is rebalanced to ensure AVL tree property is met.

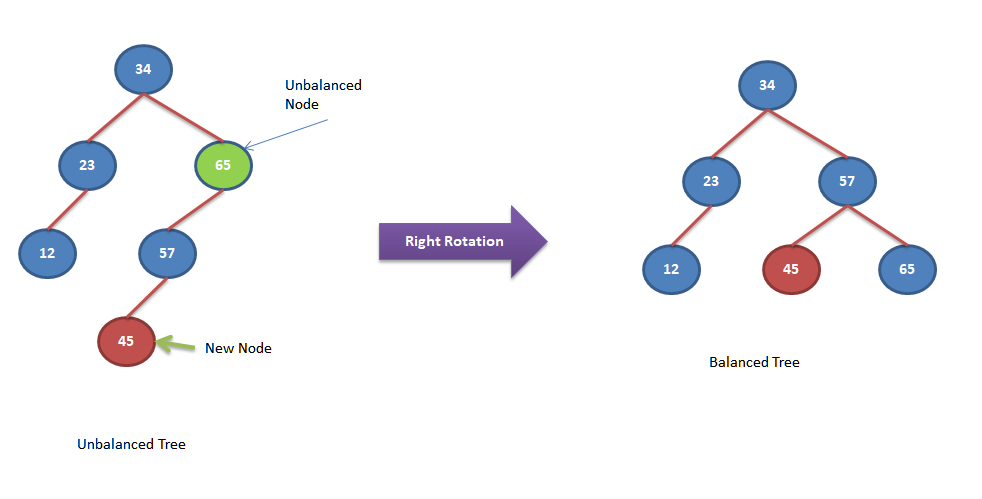
Let’s look into few insertion examples and self balancing of nodes.

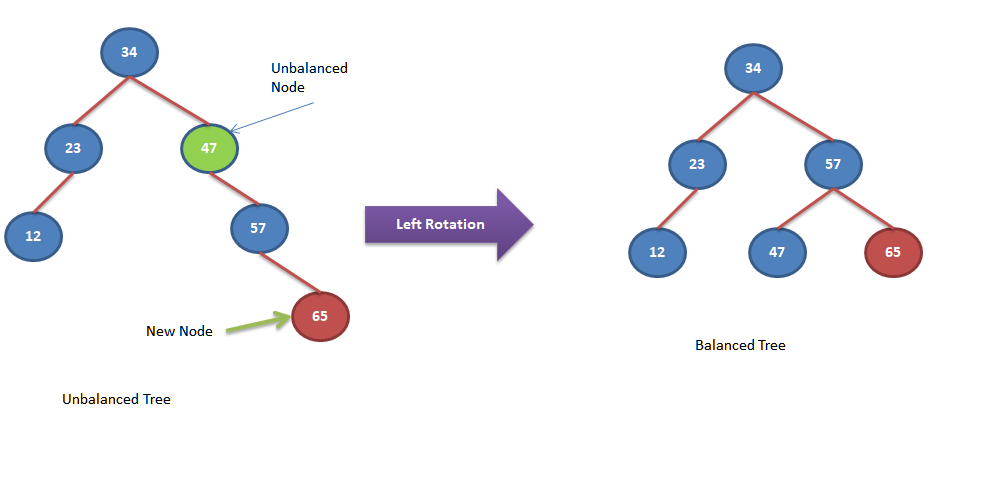
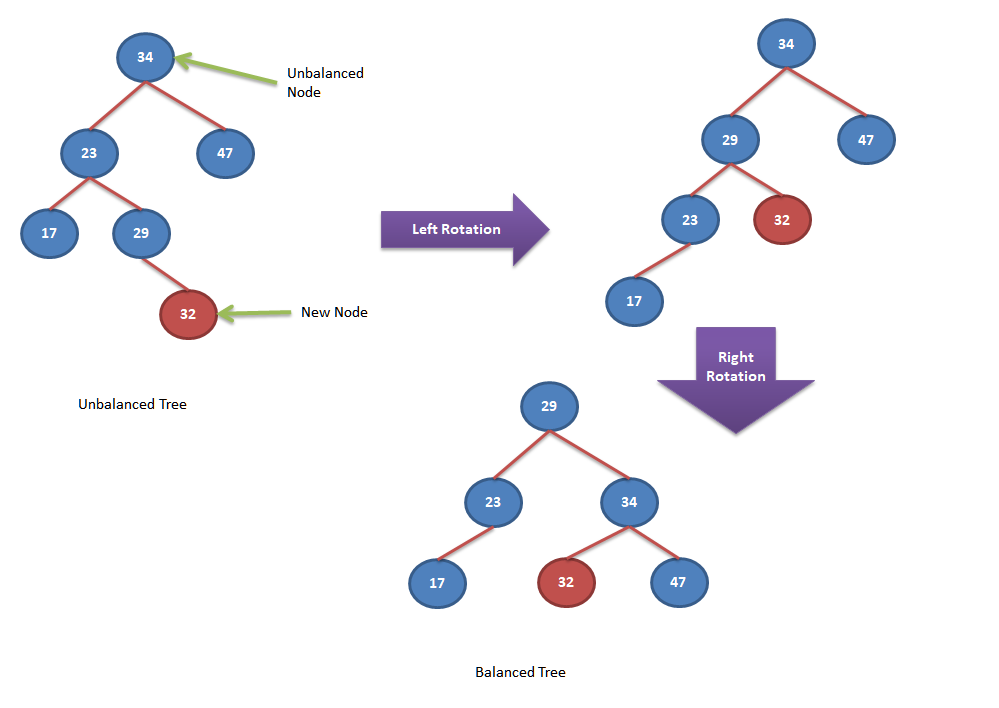
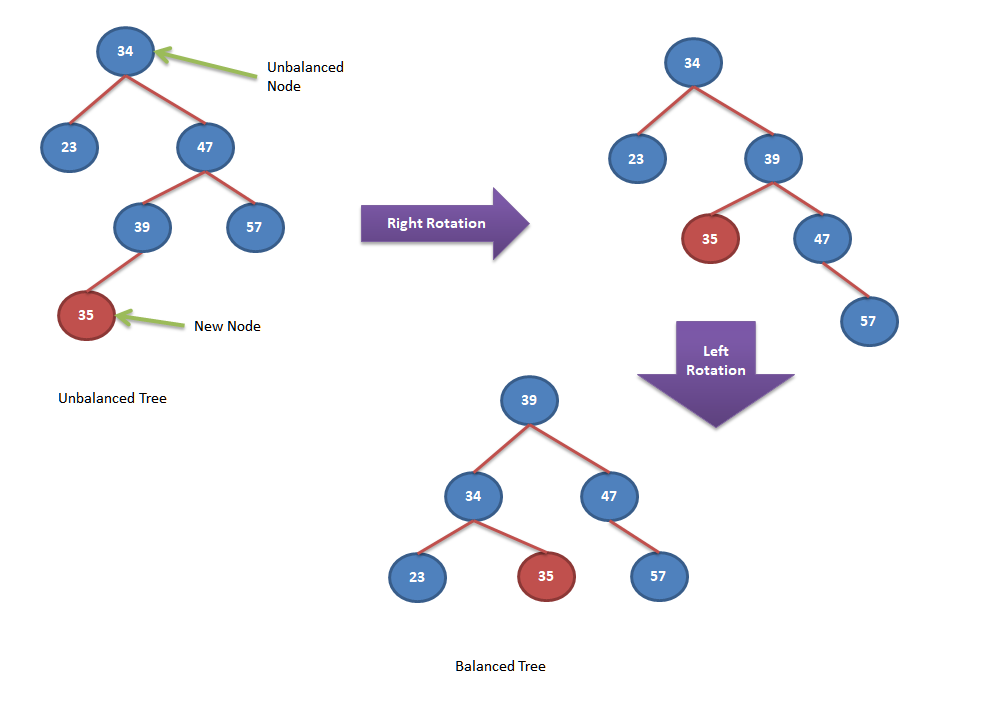
Algorithm

  • Add new node into this correct place using Binary Search Tree Insertion algorithm.
  • While returning from the recursive insertion function, check each node height balance formula.
  • If any node is found to be unbalanced then
    • if left subtree of the node is higher and new node data is lesser than node’s left child data
    • if left subtree of the node is higher and new node data is higher than node’s left child data
    • if right subtree of the node is higher and new node data is lesser than node’s right child data
    • if right subtree of the node is higher and new node data is higher than node’s right child data
  • return node.

Before going ahead let’s look into following article

Let’s look into the sample code for inserting of a node in AVL Tree.

template <typename T>
AVL<T>* insert_in_avl (AVL<T>* node, AVL<T>* new_node)
{
    if (!node)
        return new_node;

    if (node -> m_data > new_node -> m_data)
    {
        if (node -> m_left)
            node -> m_left = insert_in_avl (dynamic_cast<AVL<T>*> (node -> m_left), new_node);
        else
            node -> m_left = new_node;
    }
    else
    {
        if (node -> m_right)
            node -> m_right = insert_in_avl (dynamic_cast<AVL<T>*> (node -> m_right), new_node);
        else
            node -> m_right = new_node;
    }
    
    node -> m_height = height_of_node (node);

    int height_balance = height_of_node (node -> m_left) - height_of_node (node -> m_right);

    if (height_balance <= 1 && height_balance >= -1)
        return node;

    /* Left subtree is higher and new node went into left subtree of the left child */
    if (height_balance > 1 && new_node -> m_data < node -> m_left -> m_data)
        return right_rotate (node);

    /* Left subtree is higher and new node went into right subtree of the left child */
    if (height_balance > 1 && new_node -> m_data > node -> m_left -> m_data)
        return left_right_rotate (node);

    /* Right subtree is higher and new node went into right subtree of the right child */
    if (height_balance < -1 && new_node -> m_data > node -> m_right -> m_data)
        return left_rotate (node);

    /* Right subtree is higher and new node went into left subtree of the right child */
    if (height_balance < -1 && new_node -> m_data < node -> m_right -> m_data)
        return right_left_rotate (node);

    return node;
}

Let’s look into the sample main function to insert a node in AVL Tree.

template <typename T>
void print_binary_tree_preorder (BinarySearchTree<T>* root)
{
    cout << " " << root -> m_data;
    if (root -> m_left)
        print_binary_tree_preorder (root -> m_left);
    if (root -> m_right)
        print_binary_tree_preorder (root -> m_right);
}

template <typename T>
void print_tree_preorder (BinarySearchTree<T>* root)
{
    cout << "Binary tree contents in preorder: ";
    print_binary_tree_preorder (root);
    cout << endl;
}

int main ()
{
    AVL<int>* root = new AVL<int> (33);
    root = insert_in_avl (root, new AVL<int> (24));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (21));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (12));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (23));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (37));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (31));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    delete_all_nodes (root);
}

Let’s analyze the output of above main function.

Binary tree contents in preorder:  33 24
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 33
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 12 33
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 12 23 33
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 12 23 33 37
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 12 23 33 31 37
Binary Search Tree is AVL: 1

admin

View all posts by admin →

You might also like

Heap sort explained with simple example

Binary Search Tree data structures explained

AVL Tree Deletion Of Node Explained With Simple Example

Leave a Reply

Your email address will not be published. Required fields are marked *