AVL Tree Explanation With Simple Examples

An AVL (Adelson-Velskii and Landis) Tree is a self balancing Binary Search Tree which has the following properties.

For any node “A”, the height of the left subtree of “A” and height of the right subtree of “A” differ by 1 at max.

In case of Binary search Trees worst case search complexity is O(n) in cases when the Binary Search Tree is skewed. In AVL tree, since heights of left and right subtree are balanced, hence search complexity improves to O(log n).

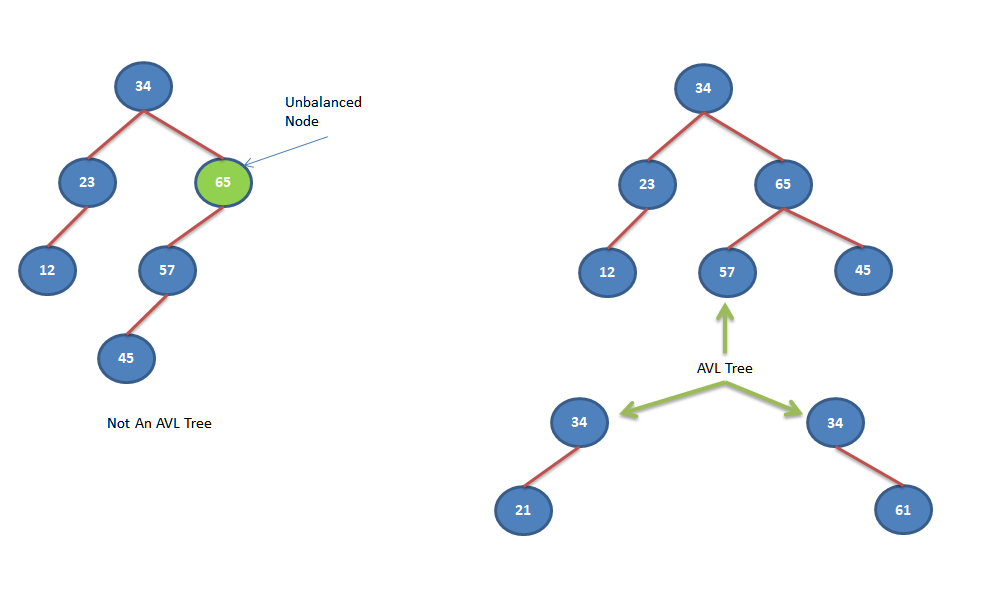
Examples of AVL Tree

Below are the some example of AVL trees.

AVL Tree Class definition

Let’s have a look into basic C++ class definition for AVL Tree.

template <typename T>
class AVL
{
    public:
        T m_data;
        AVL* m_left;
        AVL* m_right;
		int m_height;

        AVL (T data);
        ~AVL ();
};

AVL Tree Class Function Implementation

Let’s have a look into all the functions/operations definition of AVL Tree Class.

Constructor/Destructor implementation

/* This constructor will be called when an isolated node is created */
template <typename T>
AVL<T>::AVL(T data): m_data(data),
                     m_left (NULL),
                     m_right (NULL)
{}

/* No dynamic allocation is being done, hence nothing to delete here */
template <typename T>
AVL<T>::~AVL ()
{}

AVL Tree Operation

AVL Tree supports all the operation of Binary Search Trees. However, while inserting or deleting an entry there might be a chance of tree becoming unbalanced. Hence, AVL Tree supports Rotation operations to self balance itself.

Rotations

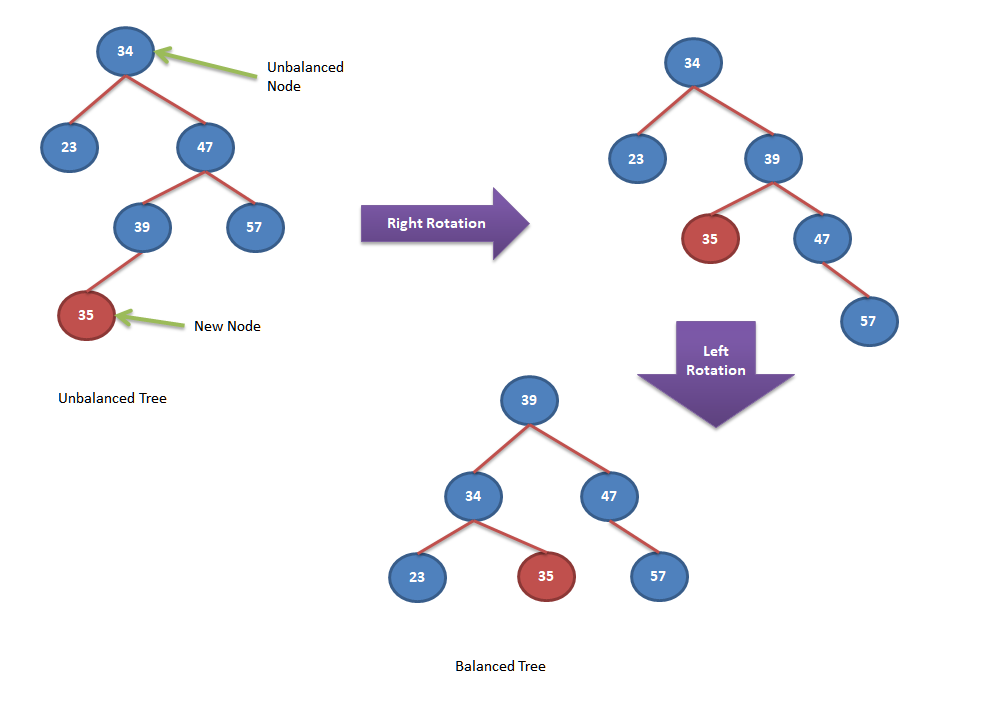
Whenever a new element is inserted into an AVL Tree, there is a chance of AVL tree becoming unbalanced.
In order to rebalance AVL tree again to satisfy the height criteria, AVL tree rotations are performed.
In order to rebalance the tree, we start at the node inserted and travel up the tree, balancing each and every node of the tree.
To balance itself, an AVL Tree can perform following four kind of rotations.

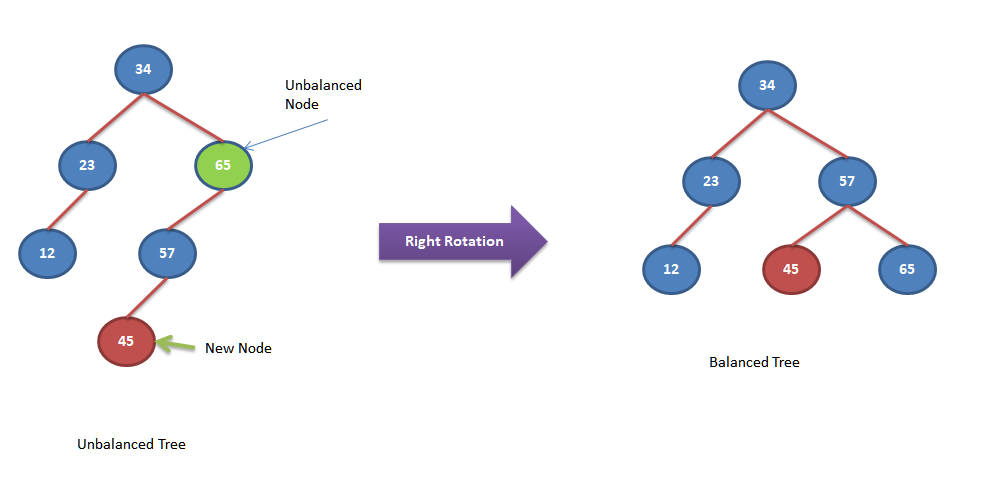
Right Rotations

In this rotation operation, left child “L” of the unbalanced node “A” replaced the unbalanced node position and unbalanced node “A” becomes the right child of the replacing node “L”. If node “L” has any existing right child then it will be moved as the left child of unbalanced node “A”. Let’s look into below example to understand it better.

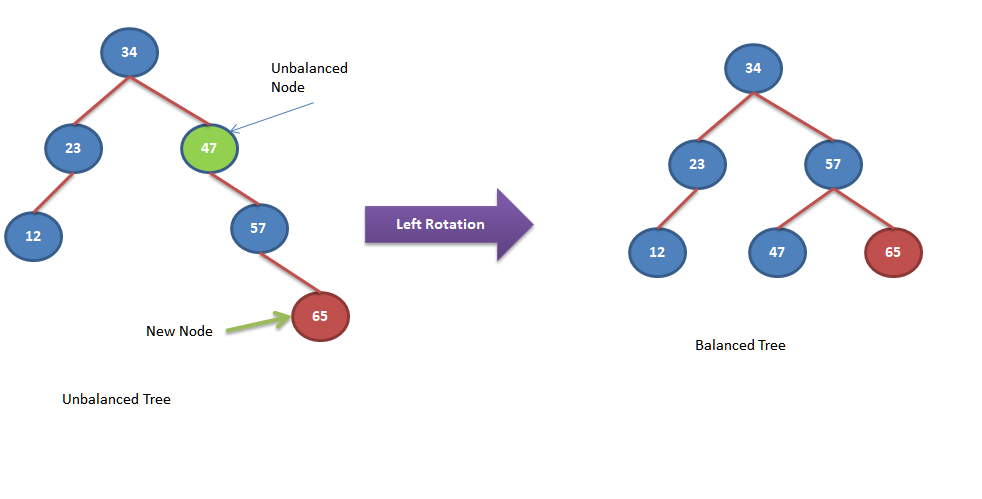
Left Rotations

In this rotation operation, right child “R” of the unbalanced node “A” replaced the unbalanced node position and unbalanced node “A” becomes the left child of the replacing node “R”. If node “R” has any existing left child then it will be moved as the right child of unbalanced node “A”. Let’s look into below example to understand it better.

Left-Right Rotations

In this case, single rotation operations are unable to rebalance the AVL Tree and hence double rotation is performed to rebalance the tree. To do so first left rotation is being performed and then right rotation is performed. This operation is usually performed when left subtree of a node has height higher than the right subtree. Let’s look into below example to understand it better.

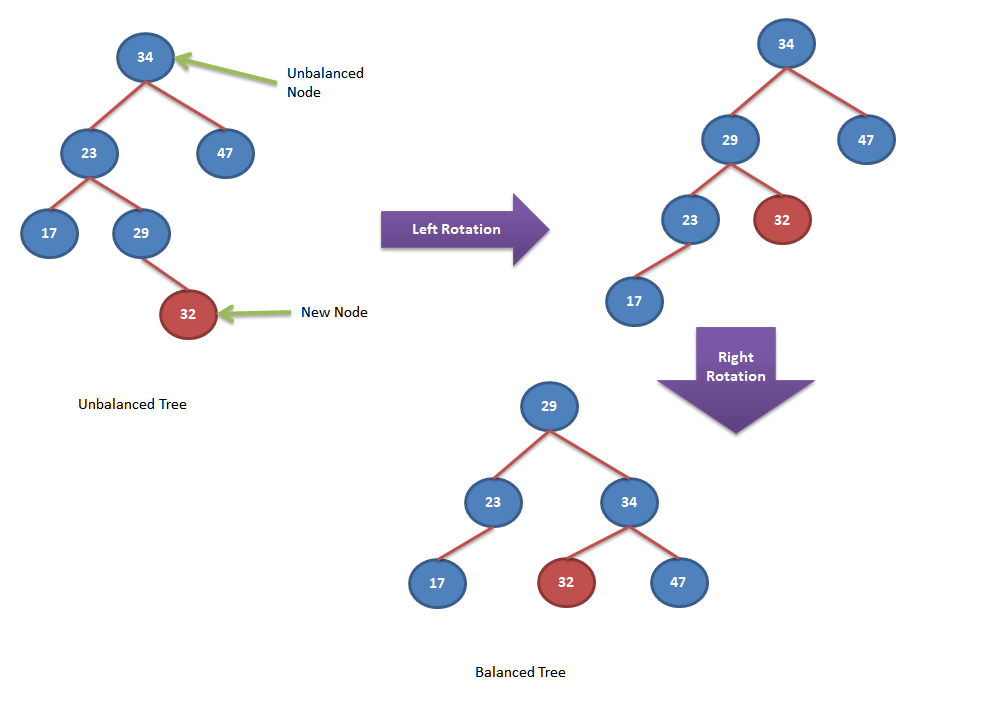
Right-Left Rotations

In this case, single rotation operations are unable to rebalance the AVL Tree and hence double rotation is performed to rebalance the tree. To do so first right rotation is being performed and then left rotation is performed. This operation is usually performed when right subtree of a node has height higher than the left subtree. Let’s look into below example to understand it better.

AVL Tree Explanation With Simple Examples

Examples of AVL Tree