AVL Tree Deletion Of Node Explained With Simple Example

An AVL (Adelson-Velskii and Landis) Tree is a self balancing Binary Search Tree which has the following properties.

For any node “A”, the height of the left subtree of “A” and height of the right subtree of “A” differ by 1 at max.

In case of Binary search Trees worst case search complexity is O(n) in cases when the Binary Search Tree is skewed. In AVL tree, since heights of left and right subtree are balanced, hence search complexity improves to O(log n). Before going ahead have a look into AVL Tree Basics.

AVL Tree Class definition

Since AVL Tree is a Binary Search Tree also, hence in all code below we have used the same property to show how to use inheritance effectively.
In below code, we have define AVL class as a derived class of Binary Search Tree Base class. Please check here for more information related to Binary Search Tree implementations before going ahead.
Let’s have a look into basic C++ class definition for AVL Tree.

template <typename T>
class BinarySearchTree
{
    public:
        T m_data;
        BinarySearchTree* m_left;
        BinarySearchTree* m_right;

        BinarySearchTree (T data);
        virtual ~BinarySearchTree ();
};

template <typename T>
class AVL: public BinarySearchTree<T>
{
    public:
        int m_height;
        AVL (T data);
        ~AVL ();
};

template <typename T>
AVL<T>::AVL (T data):BinarySearchTree<T> (data), m_height (0)
{}

template <typename T>
AVL<T>::~AVL ()
{}

Deleting an element

In order to delete an element in AVL tree, first we need to find the node in the existing AVL using Binary Search Tree deletion Algorithm. After deleting the element, all the nodes in the path from root to this deleted node will be checked for balanced condition required for AVL tree. If any node in AVL Tree is found to be unbalanced then using

methods AVL tree node is rebalanced to ensure AVL tree property is met.

Let’s look into few deletion examples and self balancing of nodes.

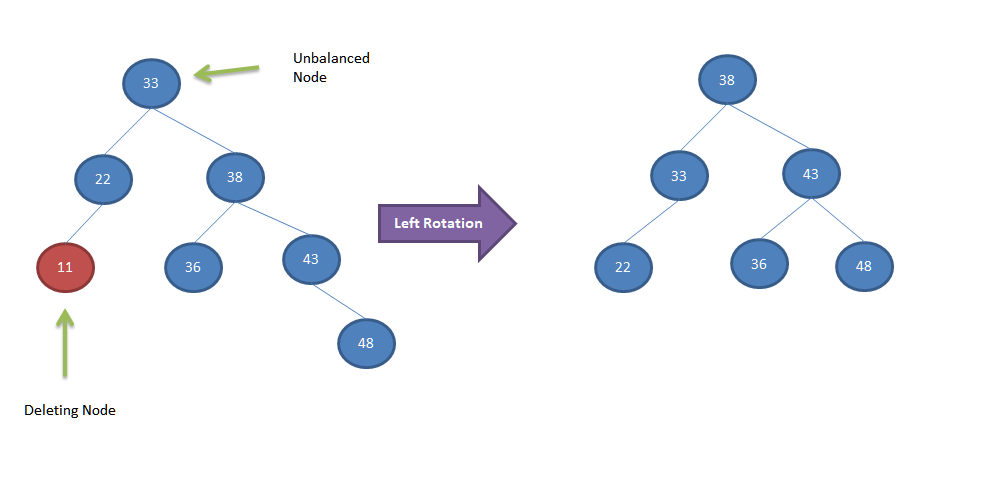
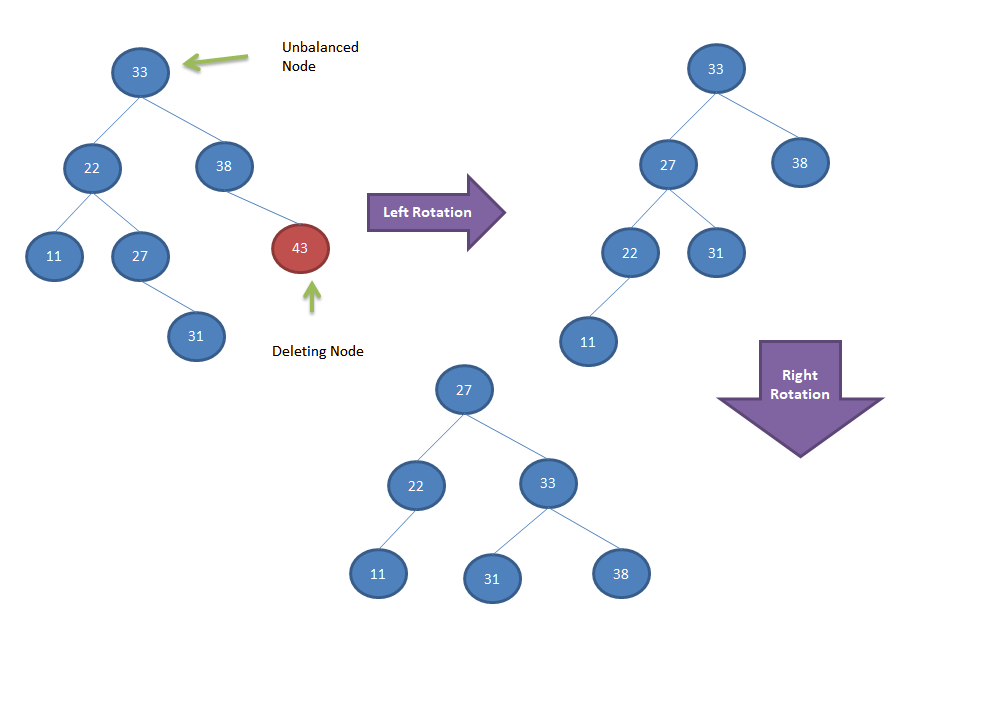
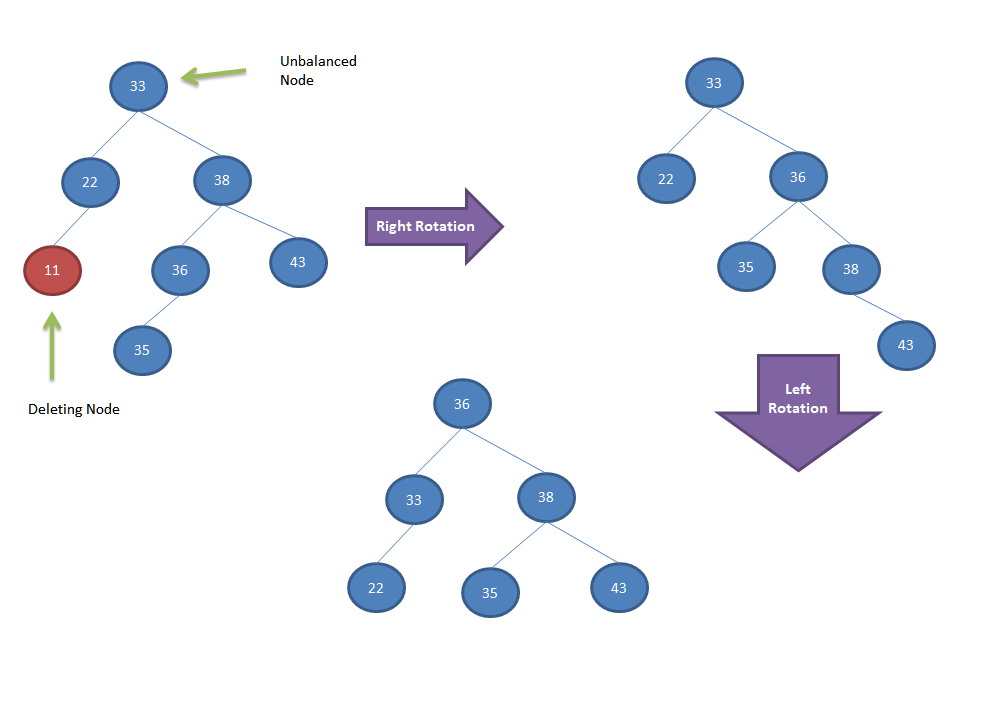
Algorithm

Delete node from the AVL Tree using Binary Search Tree Deletion algorithm.
While returning from the recursive deletion function, check each node height balance formula.
If any node is found to be unbalanced then
- if left subtree of the node is higher and new node data is lesser than node’s left child data
  - Perform right rotation to balance the nodes.
- if left subtree of the node is higher and new node data is higher than node’s left child data
  - Perform left right rotation to balance the nodes.
- if right subtree of the node is higher and new node data is lesser than node’s right child data
  - Perform right left rotation to balance the nodes.
- if right subtree of the node is higher and new node data is higher than node’s right child data
  - Perform left rotation to balance the nodes.
return node.

Before going ahead let’s look into following article

Let’s look into the sample code.

template <typename T>
AVL<T>* delete_in_avl (AVL<T>* node, T data)
{
    if (!node)
        return node;

    if (node -> m_data < data)
        node -> m_right = delete_in_avl (dynamic_cast<AVL<T>*> (node -> m_right), data);
    else if (node -> m_data > data)
        node -> m_left = delete_in_avl (dynamic_cast<AVL<T>*> (node -> m_left), data);
    else
    {
        if (node -> m_left)
        {
            AVL<T>* temp = NULL;
            if (node -> m_right)
            {
                temp = dynamic_cast<AVL<T>*> (node -> m_right);
                temp = insert_in_avl (temp, dynamic_cast<AVL<T>*> (node -> m_left));
            }
            else
            {
                temp = dynamic_cast<AVL<T>*> (node -> m_left);
            }
            delete node;
            node = temp;
        }
        else
        {
            if (node -> m_right)
            {
                AVL<T>* temp = dynamic_cast<AVL<T>*> (node -> m_right);
                delete node;
                node = temp; 
            }
            else
            {
                delete node;
                return NULL;
            }
        }
    }
    
    node -> m_height = height_of_node (node);

    int height_balance = height_of_node (node -> m_left) - height_of_node (node -> m_right);

    if (height_balance <= 1 && height_balance >= -1)
        return node;

    if (height_balance > 1 && height_of_node (node -> m_left) >= 0)
        return right_rotate (node);
    if (height_balance > 1 && height_of_node (node -> m_left) < 0)
        return left_right_rotate (node);
    if (height_balance < -1 && height_of_node (node -> m_right) <= 0)
        return left_rotate (node);
    if (height_balance < -1 && height_of_node (node -> m_right) > 0)
        return right_left_rotate (node);

    return node;
}

Let’s look into the sample main function to insert a node in AVL Tree.

template <typename T>
void print_binary_tree_preorder (BinarySearchTree<T>* root)
{
    cout << " " << root -> m_data;
    if (root -> m_left)
        print_binary_tree_preorder (root -> m_left);
    if (root -> m_right)
        print_binary_tree_preorder (root -> m_right);
}

template <typename T>
void print_tree_preorder (BinarySearchTree<T>* root)
{
    cout << "Binary tree contents in preorder: ";
    print_binary_tree_preorder (root);
    cout << endl;
}

int main ()
{
    AVL<int>* root = new AVL<int> (33);
    root = insert_in_avl (root, new AVL<int> (24));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (21));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (12));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (23));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (37));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = insert_in_avl (root, new AVL<int> (31));
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = delete_in_avl (root, 37);
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;
    
    root = delete_in_avl (root, 24);
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = delete_in_avl (root, 23);
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    root = delete_in_avl (root, 31);
    print_tree_preorder (root);
    cout << "Binary Search Tree is AVL: " << isAVL (root) << endl;

    delete_all_nodes (root);
}

Let’s analyze the output of above main function.

Binary tree contents in preorder:  33 24
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 33
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 12 33
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 12 23 33
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 12 23 33 37
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 12 23 33 31 37
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  24 21 12 23 33 31
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  31 21 12 23 33
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  31 21 12 33
Binary Search Tree is AVL: 1
Binary tree contents in preorder:  21 12 33
Binary Search Tree is AVL: 1

AVL Tree Deletion Of Node Explained With Simple Example

AVL Tree Class definition

Deleting an element

Algorithm

admin

Leave a Reply Cancel reply

AVL Tree Class definition

Deleting an element

Algorithm

admin

You might also like

Binary Tree Level Order Traversal Explained With Simple Example

Connected Graph Property Explained With Simple Example

Boundary Traversal Of A Binary Tree

Leave a Reply Cancel reply